数学が得意な国として有名なインド。
しかし、古代インドはエジプトやバビロニアと比較して、優れた数学力を持っていませんでした。
この記事では、インダス文明を起源とした古代インドの歴史やアラビア数字の祖先であるブラーフミー数字について解説。
古代インドの数学が発展しなかった理由は、アーリヤ人の民族性にありました。
| 時代 | B.C.2600年頃~B.C.330年頃 |
| 場所 | インド |
古代インド数学の歴史
四大文明の一つ、インダス文明を起源とするインド。
まずは、紀元前におけるインドの歴史を背景に、数学がどの程度発展していたのかを見てみましょう。
インダス文明は約1000年で衰退した
紀元前2600年頃、インダス文明はインダス川流域で興りました。
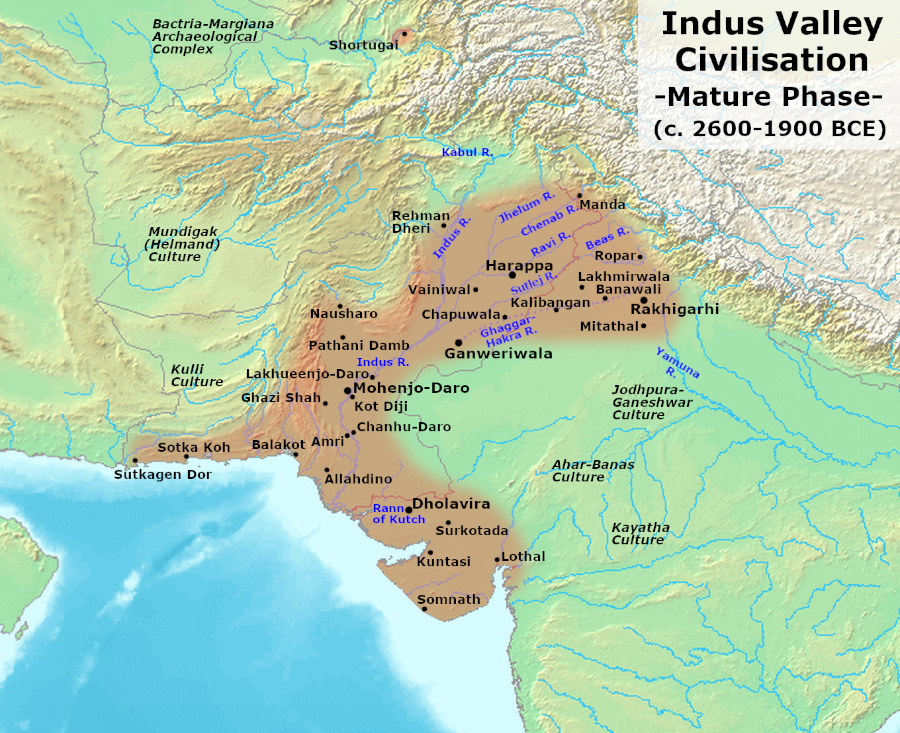
(出典:Avantiputra7, CC BY-SA 3.0, via Wikimedia Commons)
しかし、エジプトやメソポタミア(バビロニア)のような発展は遂げられず、紀元前1800年頃までにはインダス文明は衰退してしまいました。
現在でも解明されていないインダス文字が存在していたこと、同時期のエジプトやバビロニアが数字を使っていたことから、インダス文明でも数字を扱うほどの数学レベルはあったと推測できます。
部族的な社会をもつアーリヤ人の進入
インダス文明が衰退してから約300年。
紀元前1500年頃、インド北西部に牧畜民であるアーリヤ人が進入し始めました。
アーリヤ人は部族的な社会をもち、雷や火などの自然神が崇拝され、様々な祭式が行われました。
紀元前1000年頃には、それらの宗教的な知識をまとめた『シュルバスートラ』が書かれ、儀式のために必要な縄の長さや縄で囲んだ図形の面積といった平面幾何学が、古代インドを代表する数学として残っています。

仏教の誕生や異民族の侵入で独自の文化が失われた
紀元前6世紀頃になり、アーリヤ人の難解な祭式や身分制度を否定したガウタマ・シッダールタ(ブッダ)は仏教を開きました。

(出典:พระมหาเทวประภาส วชิรญาณเมธี (ผู้ถ่าย-ปล่อยสัญญาอนุญาตภาพให้นำไปใช้ได้เพื่อการศึกษาโดยอยู่ภา่ยใต้ cc-by-sa-3.0) ผู้สร้างสรรค์ผลงาน/ส่งข้อมูลเก็บในคลังข้อมูลเสรีวิกิมีเดียคอมมอนส์ – เทวประภาส มากคล้าย, CC BY-SA 3.0, via Wikimedia Commons)
仏教が人々に浸透していくと共に、アーリヤ人の祭式、すなわち古代インド元来の平面幾何学は徐々に衰退していきました。
そして、紀元前330年頃になると、西からアレクサンドロス大王がインドに迫ります。

(出典:Berthold Werner, Public domain, via Wikimedia Commons)
これを機に、ギリシャ人勢力がインドに侵入したり、ローマとの交易を行う王朝が誕生したりと、ギリシャ文化がインドに入り込み、古代インド特有の数学は廃れてしまいました。
古代インドの数字「ブラーフミー数字」
インドで最も古い文字は、紀元前2600年~1900年使われていた「インダス文字」であり、解読が進んでいないため、数字が存在していたかどうかは定かではありません。
そのため現在わかっている範囲で、インドで使われていた最も古い数字は「ブラーフミー数字」となっています。
現在のアラビア数字の祖先
ブラーフミー数字は、古代インドで紀元前400年頃から紀元後600年頃まで使われていました。
その後、「サンスクリッド数字」や「デーヴァナーガリー数字」などを経て、現在我々が使っている「アラビア数字」へと変化しました。
12世紀にはアラビア数字がヨーロッパに伝わり、レオナルド・フィボナッチ(Leomardo Fibonacci , 1180年頃~1250年頃)の『算盤の書』や、1445年頃の活版印刷機の発明により、全世界に広がります。

(出典:unknown 19th-century artist, Public domain, via Wikimedia Commons)
16世紀ごろにはアラビア数字は今と同じ形に整えられ(図5左)、インドの記数法が世界中で使われるようになりました。
(出典:Olaus Magnus, Public domain, via Wikimedia Commons)
数字は全部で20種類
ブラーフミー数字は$~1~$ から$~9~$に加え、 $~10~,~20~,~30~,~\cdots~,~90~$、さらには$~100~,~1000~$を表す 20種類の数字(記号)が用意されていました。

エジプトやバビロニアと違い、$~1~$から$~9~$までの数字が用意されていたという点で、現在のアラビア数字に繋がるものがあります。
乗法的記数法でさまざまな数を表した
エジプトのヒエログリフやバビロニアの楔型文字といった、位に基づいた記数法とは異なり、ブラーフミー数字は「乗法的記数法」が採用されました。
乗法的記数法とは、数字と数字をかけ合わせることで、用意されていない数字を新たに作るという表し方で、古代中国でも使われました。

基本は既存の数字のかけ算
数字を新たに作るというのはどういうことなのか?
下の例を見てみましょう。
- $~400~$は$~100 \times 4~$なので、$~100~$と$~4~$を組み合わせた数字となる。(図7左)
- $~6000~$は$~1000 \times 6~$なので、$~1000~$と$~6~$を組み合わせた数字となる。(図7中)
- $~10000~$は$~1000 \times 10~$なので、$~1000~$と$~10~$を組み合わせた数字となる。(図7右)
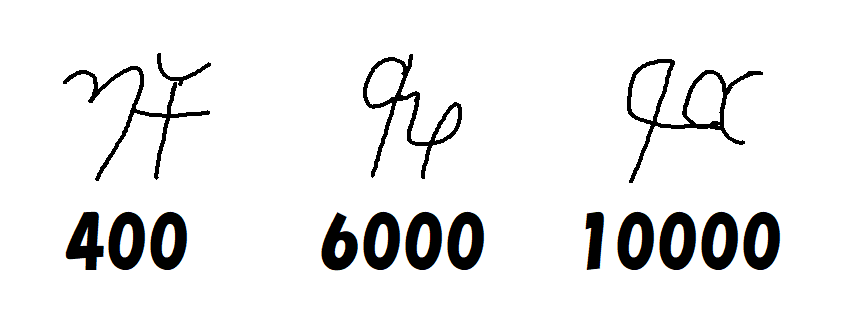
この例からもわかるように、既存の数字どうしを合わせ書くことで新たな数字を表していました。
×2 や×3 だけは横棒を1,2本追加する
ただし、かける数が$~2~$や$~3~$の場合には、特殊な考え方をします。
- $~200~$は$~100~$に$~100~$を$~1~$つ加えた数なので、$~100~$と$~1~$を組み合わせた数字となる。(図8左)
- $~300~$は$~100~$に$~100~$を$~2~$つ加えた数なので、$~100~$と$~2~$を組み合わせた数字となる。(図8右)
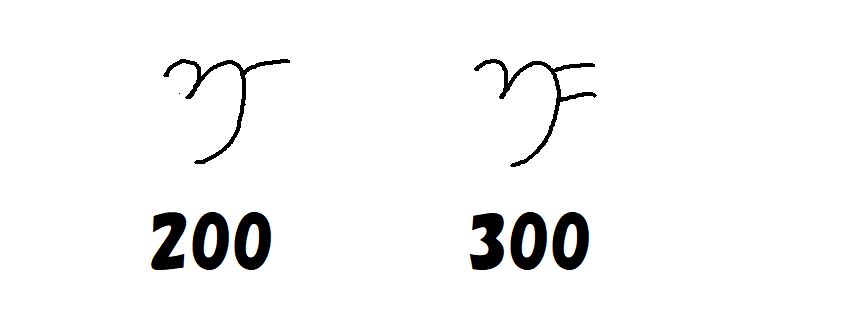
$~2000~$や$~3000~$についても同様の考え方で表します。
ただ、$~400~$や$~4000~$に関しては、先ほどのかけ算の考え方を使うので、注意が必要です。
まとめ・参考文献
古代インドの数学の特徴やブラーフミー数字について解説してきました。
- 祭式を重視するアーリヤ人により、古代インドでは平面幾何が発達した。
- 古代インドの数学は儀式書『シュルバスートラ』に残っている。
- 古代インドから使われたブラーフミー数字は、アラビア数字の元となっている。
古代インドの数学自体には、エジプトやバビロニアに比べて目を見張るような功績が残っていないものの、ブラーフミー数字は現在の数字の元となった大きな発明です。
次の記事では、宗教書『シュルバスートラ』に残る問題を解説します。



合字だと、微妙にもとの数字から変化しているのが気になるにゃ。



勝手な予想だけど、そうすることで合字であるということがわかりやすかったのでは?
$~500=100 \times 5~$を分けて書くと、$~105~$になっちゃうから。
参考文献(本の紹介ページにリンクしています)
- 『カッツ 数学の歴史』,pp.7-11
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.205-207
- 『数学史 数学5000年の歩み』,pp.130-131
- 『ずかん 数字』,pp.86-99
- 木村靖二・岸本美緒・小松久男(2022)『詳説 世界史 改訂版』,pp52-56,山川出版社.
- 西野芳治(2003)『古代インドにおける数字と記数法に関する一考察』(http://www.osaka-shinai.ac.jp/library/kiyo/37/nishino.pdf)

コメント
コメント一覧 (2件)
インド数学といえば、まずは「0の発見者」として知られるブラフマグプタがいます。
和算があまり知られていないのと同じように、「ヨーロッパ数学が東方世界の数学についてあまり関心を向けなかっただけ」と私は解釈しています。
ブラフマグプタは「0÷0=0」と考えていたとされますが、現代では「不定」とされているので間違ってはいません(笑)。「0÷0=1」だろうが「0÷0=n」だろうが、「なんでもあり」です。
それよりも「空位を表す0」ではなく、「数としての0」を発想したところがスゴいと思います。
現代では、物理学者にインド系の著名人が多く、チャンドラセカールなどが知られていますが、なんといってもラマヌジャンがいるので、インド数学の伝統が現代の数学に与えた影響は大きいと考えています。
島田正雄様
コメントありがとうございます。
そのうちこのサイトでも取り上げることになるかと思いますが、ブラフマグプタの功績は大きいですよね。
バビロニアやマヤとかでも、記号としての0は使っていたものの、計算に使用するという発想は彼が最初。
それをアラビア経由でヨーロッパに伝える役割を果たしたアル・フワーリズミーも大きな影響力を果たしたと思っています。