古代インド数学では、他の四大文明と比べても大きな成果がありませんでした。
エジプトの『リンド・パピルス』やバビロニアの多数の粘土板のような記録もなく、古代インド数学のことがわかる書物は儀式書『シュルバスートラ』のみとなっています。
この記事では、シュルバスートラ自体とそこに載っている平面幾何について解説。
儀式を大切にしたアーリヤ人が、儀式に使える数学を研究していました。
| 時代 | B.C.1000年頃~B.C.330年頃 |
| 場所 | インド |
儀式書『シュルバスートラ』とは?
古代インドに関して、インダス文明で使われていたインダス文字は依然解読されていないため、現在知られている最古のインド数学は紀元前1000年頃の数学になります。
その貴重な文献となっているのが、儀式書『シュルバスートラ』です。
『シュルバスートラ』はアーリヤ人の儀式書
『シュルバスートラ』は、紀元前1000年頃に、その時インドを支配していたアーリヤ人の言語で書かれた宗教書です。
「シュルバ」は「測定用の縄」を、「スートラ」は「宗教的儀式」を意味していて、儀式をする際に必要な縄の張り方や、その縄によって囲まれた領域の面積といった平面幾何に関する内容が多く載っています。
具体的な内容としては、長さが$~3~,~4~,~5~$や$~5~,~12~,~13~$のような3つの組の数(ピタゴラス数)を長さにとった3本の縄を用いることで直角が作れる、といった実用的なものがほとんどでした。
『シュルバスートラ』は古代インド数学の手がかり
なぜ儀式書から古代インド数学を紐解いているかと言うと、エジプトのパピルスやバビロニアの粘土板のような数学書類が1つも残っていなかったからです。
そのため、『シュルバスートラ』は儀式書と言えど、古代インドの数学の様子を窺い知る大変貴重な資料となっています。
また、他の宗教的な書物の中には、大きな数や10進法についての記述があったため、宗教や儀式の中で必要な最低限の数学のみが古代インドで必要とされていたことがわかります。
長方形を正方形にする方法
『シュルバスートラ』の中の有名な話題の1つとして、与えられた長方形を正方形に等積変形する方法が説明されていました。
補助長方形を使って作図する
『シュルバスートラ』では、以下のような手順で、コンパスと定規のみを用いた作図をしていました。
$~AC < AD~$の長方形$~ABCD~$に関して、$~AB~$を1辺とする正方形$~ABEF~$を長方形の内部に作る。
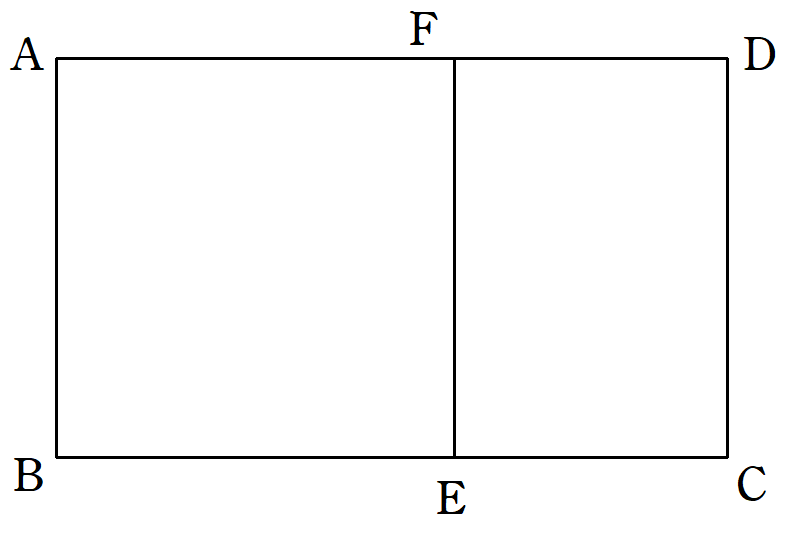
線分$~CE~,~DF~$の中点をそれぞれ$~G~,~H~$とし、$~FH~$を一辺とする正方形$~FHIJ~$を長方形$~ABCD~$の外部に作る。また、$~HG~$を結ぶ。
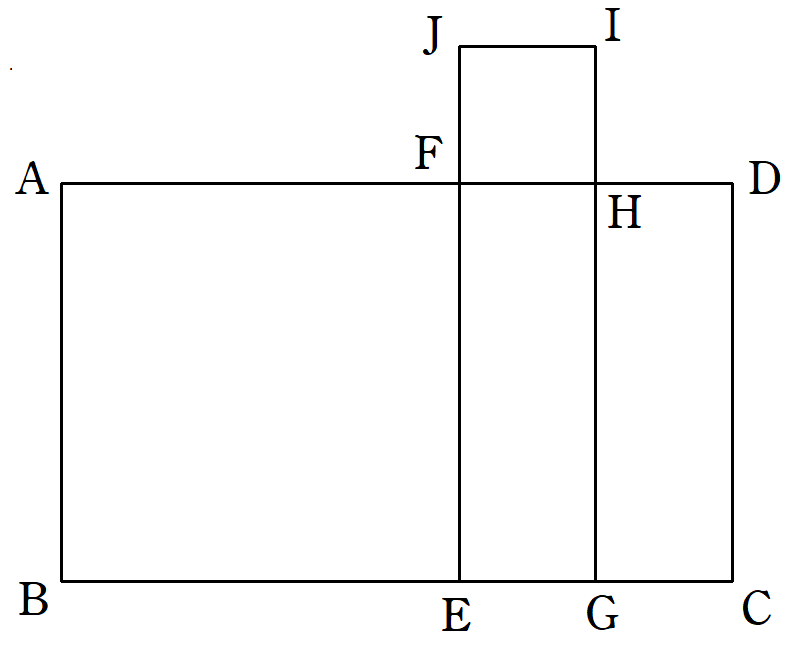
ここで、$~KL=FH~,~KM=IG~$を満たす長方形$~KLMN~$を別に作図する。
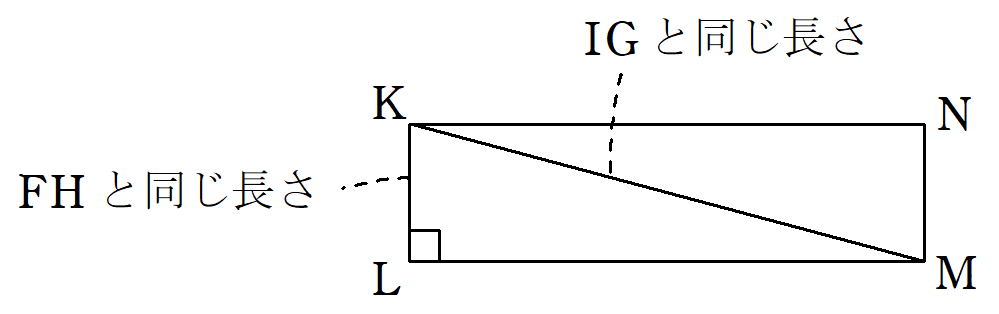
このとき、$~LM~$を一辺とする正方形の面積は、長方形$~ABCD~$の面積と等しくなる。
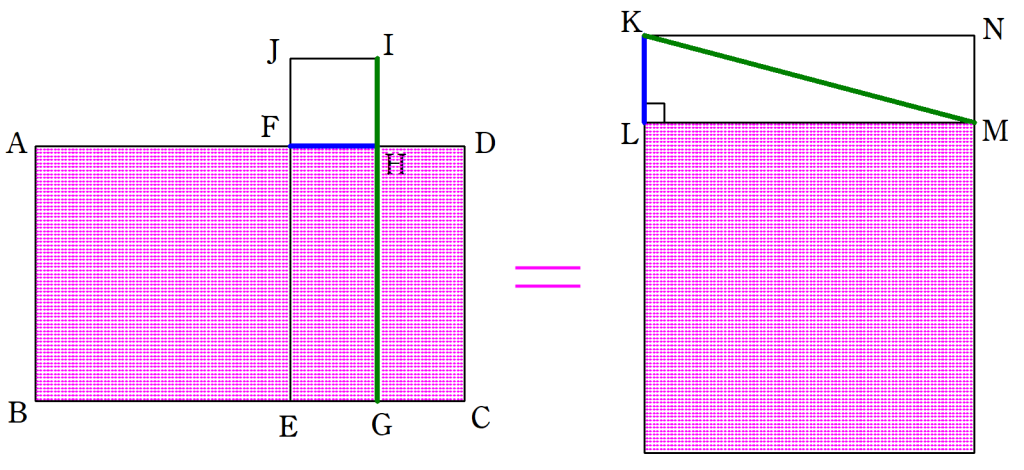
図3で出てきたような補助長方形を使うところが、作図を複雑なものにしています。
ただ、この方法で本当に長方形から正方形への等積変形ができているのでしょうか?
古代インド人も理解していた作図の根拠
先ほどの作図方法の正しさを、数式を使って証明をしてみましょう。
$~AB=a < b=AD~$とする。
このとき、次のように辺の長さが求まる。
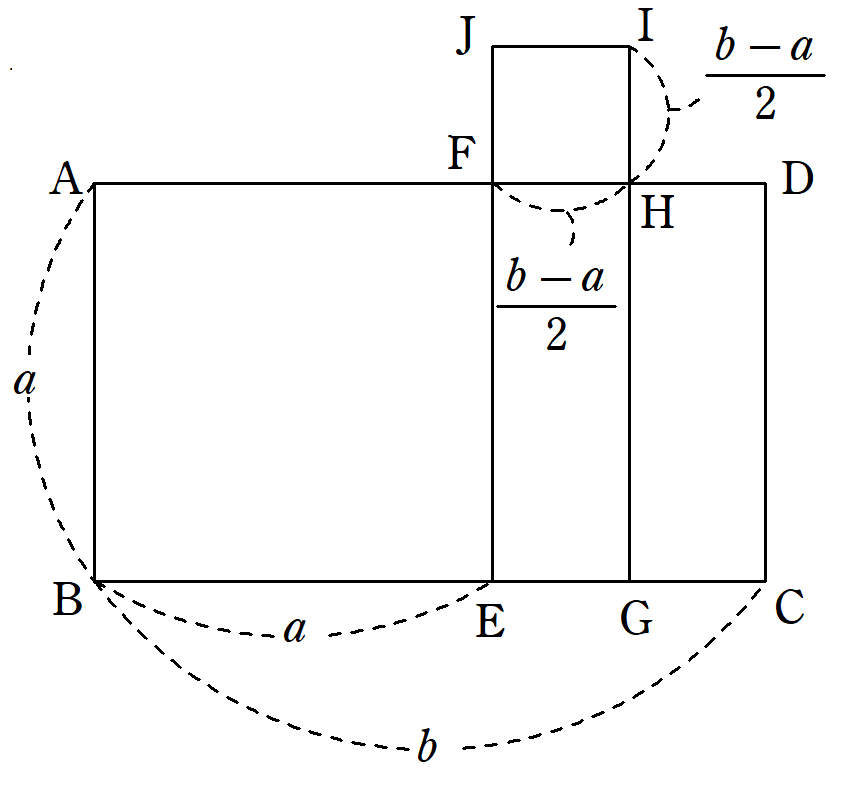
このとき、
IG=\frac{b-a}{2}+a=\frac{a+b}{2}となり、長方形$~KLMN~$は次のように作図されることとなる。
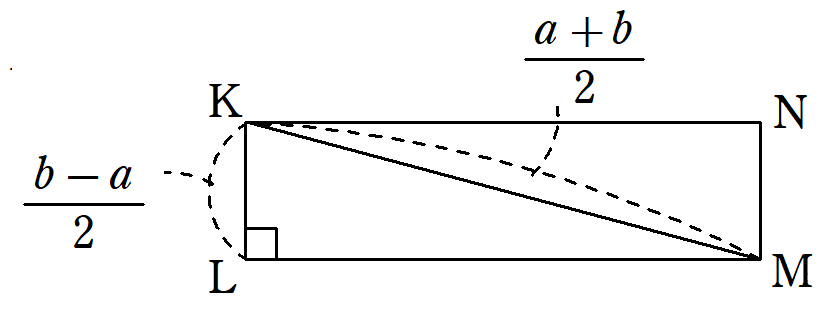
図6で三平方の定理を使うと、
\begin{align*}
LM^2+\left( \frac{b-a}{2} \right)^2&=\left( \frac{a+b}{2} \right)^2 \\
\\
4LM^2+b^2-2ab+a^2&=a^2+2ab+b^2 \\
\\
4LM^2&=4ab \\
\\
LM^2&=ab
\end{align*}となるため、$~LM~$を一辺とする正方形の面積は$~ab~$。
これは長方形$~ABCD~$の面積に一致する。$~~\blacksquare~$
以上により、作図方法が正しいことがわかりました。
『シュルバスートラ』の中には、長さが$~3~,~4~,~5~$や$~8~,~15~,~17~$といったピタゴラス数の長さの縄で、直角三角形が作れるといった記述があることから、紀元前のインド人も三平方の定理を理解していたうえで、この作図方法が論理的に正しいことを知っていたと思われます。
2つの正方形を1つにする方法
『シュルバスートラ』には、2つの正方形を合わせた面積をもつ正方形の作図方法も登場します。
2つの直角三角形を移動させるだけの作図
大小2つの正方形の面積の和を、1つの正方形で表すための作図方法は、以下の図で提示されました。
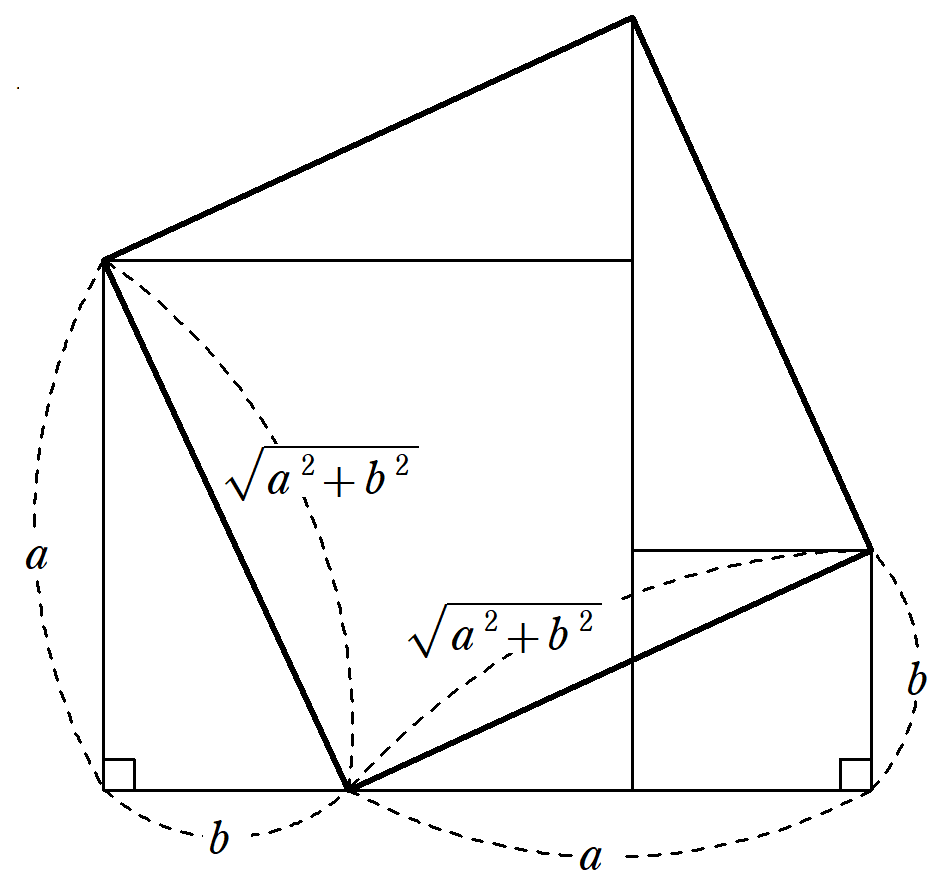
左下の直角三角形と右下の直角三角形を、それぞれ右上と左上に移動させることで、2つの正方形の面積を合わせた、1つの大きな正方形を作ることができる。
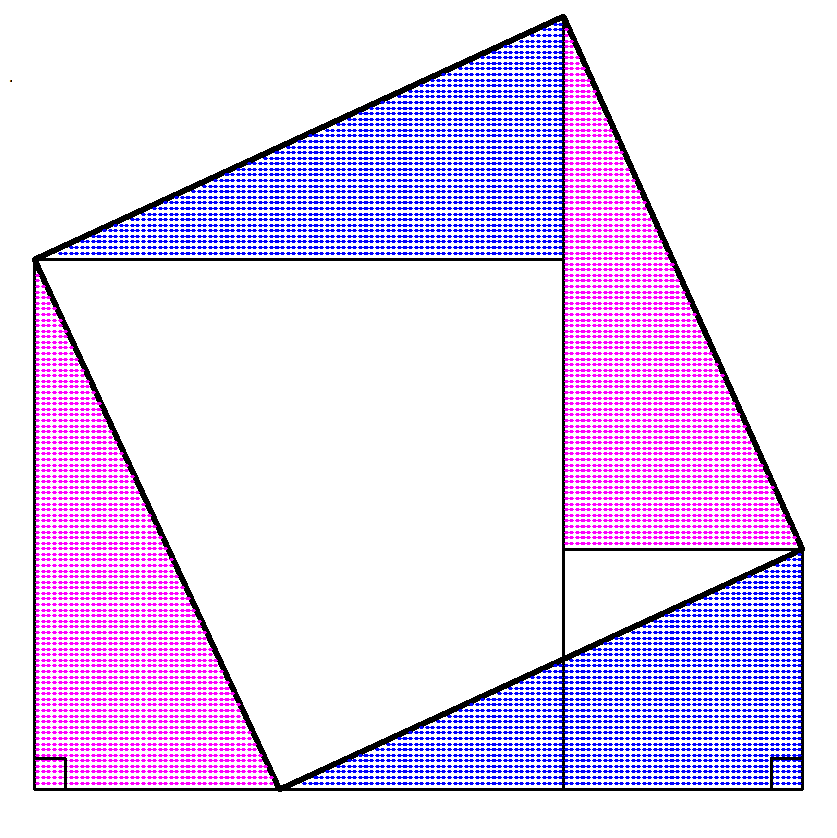
証明の根拠は”見ればわかる”ということになりますが、もとの2つの正方形の一辺を$~a~,~b~$として、数式で解決すると、下の図8のようになります。
作図を応用して√2の値を求めていた
2つの同じ大きさの正方形を用意し、2つの正方形を1つの正方形にするための作図を利用することで、次のような図ができます。
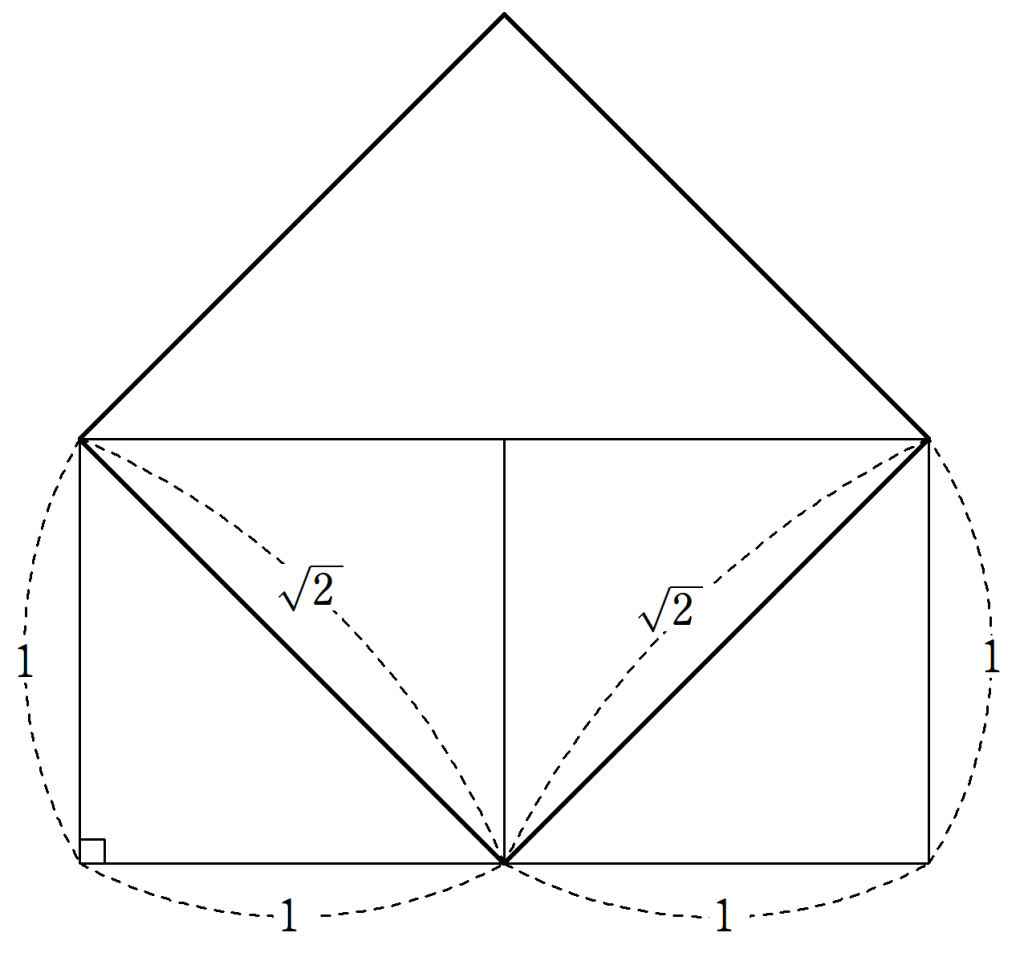
これにより、$~\sqrt{2}~$の近似値が求められました。
『シュルバスートラ』に載っていたのは、次のような値です。
\sqrt{2} \fallingdotseq 1+\frac{1}{3}+\frac{1}{3\times 4}-\frac{1}{3 \times 4 \times 34}これを小数に直すと、$~1.4142156 \cdots~$であり、小数第5位まで一致しています。
計算の手順は解明されていませんが、単位分数の和と差で表されているあたり、エジプトの影響があったのかもしれません。

まとめ・参考文献
古代インドの儀式書『シュルバスートラ』の内容について解説してきました。
- 『シュルバスートラ』は祭壇等での縄の張り方を解説した儀式書。
- 古代インドでは、儀式の際に必要な平面幾何が発達していた。
- 古代インドでは三平方の定理が知られ、等積変形の作図の根拠になっている。
儀式書でしか知りえないものの、平面幾何だけはそれなりの知識が残っている古代インド。
$~0~$の発見をはじめとする、数学国インドとしての一面は紀元後を待つことになります。
次の記事からは、四大文明最後の場所となる、古代中国の数学について解説します。


それはわからないけど、宗教書でこのレベルなのだから、この時代の数学書が残っていたら、さぞレベルが高かっただろうね。
参考文献(本の紹介ページにリンクしています)
- 『カッツ 数学の歴史』,pp.7-11
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.205-207
- 『数学史 数学5000年の歩み』,pp.130-131
- 『ずかん 数字』,pp.86-99
- 西野芳治(2003)『古代インドにおける数字と記数法に関する一考察』(http://www.osaka-shinai.ac.jp/library/kiyo/37/nishino.pdf)

コメント
コメント一覧 (2件)
「シュルバスートラ」の「スートラ」って、「経」(=お経)みたいなものなので、竹簡とか木簡とか、そういう意味だったんじゃないだろうかと思います(でなければ、「経典」「書物」)。「シュルバ」が何かという点に興味があります。
紐を使った測量法は古代エジプトや古代バビロニアでも普及していたという話はけっこうあって(岐阜県立東高校の亀井喜久男先生のぺージ(http://www.ctk.ne.jp/%7Ekamei-ki/)が情報豊富です)、ナイル河もチグリス=ユーフラテス河もインダス河もけっこう暴れ河なので、農地の境界がわからなくなっちゃうんで測量が発達したという事情があります。黄河文明も似たようなものだという説もあります。
島田正雄様
コメントありがとうございます。
スートラの意味を初めて知りました。
四大文明と河川は切っても切れない関係ですよね。
ナイル川の氾濫が幾何学(geometry)の語源につながっていますが、四大文明各地でも同じような状況が確かに推測できそうです。