紀元前6000年頃に興った中国文明。
しかし、紀元前の中国の数学を知るための資料はほとんど残っておらず、紀元前200年頃に書かれた『周髀算經』や『九章算術』が最も古い文献とみなされています。
エジプトやバビロニアでは、紀元前1000年代の数学の記録が残っているのに対し、中国においては同じくらいの時代までさかのぼることができません。
その理由は、紀元前221年に中国を統一した秦の始皇帝にありました。
この記事では、古代中国が歴史をさかのぼれない理由を含めつつ、数学に関連する歴史の流れを大まかに解説していきます。
| 時代 | B.C.6000年頃~B.C.200年頃 |
| 場所 | 中国 |
失われた5800年間
四大文明の1つである中国文明が興ったのは、紀元前6000年頃。
それに対して、紀元前の数学がわかる最古の資料は、紀元前200年頃のものとなっています。
エジプトの『リンド・パピルス』(紀元前1650年頃)、バビロニアの粘土板(紀元前2000年頃から)と比較しても、違和感がある中国特有の事情をまずは紐解きます。
秦が登場するまでは争いの歴史
黄河や長江のほとりで人々が農耕を始めた紀元前6000年頃、四大文明の1つである中国の文明が興りました。
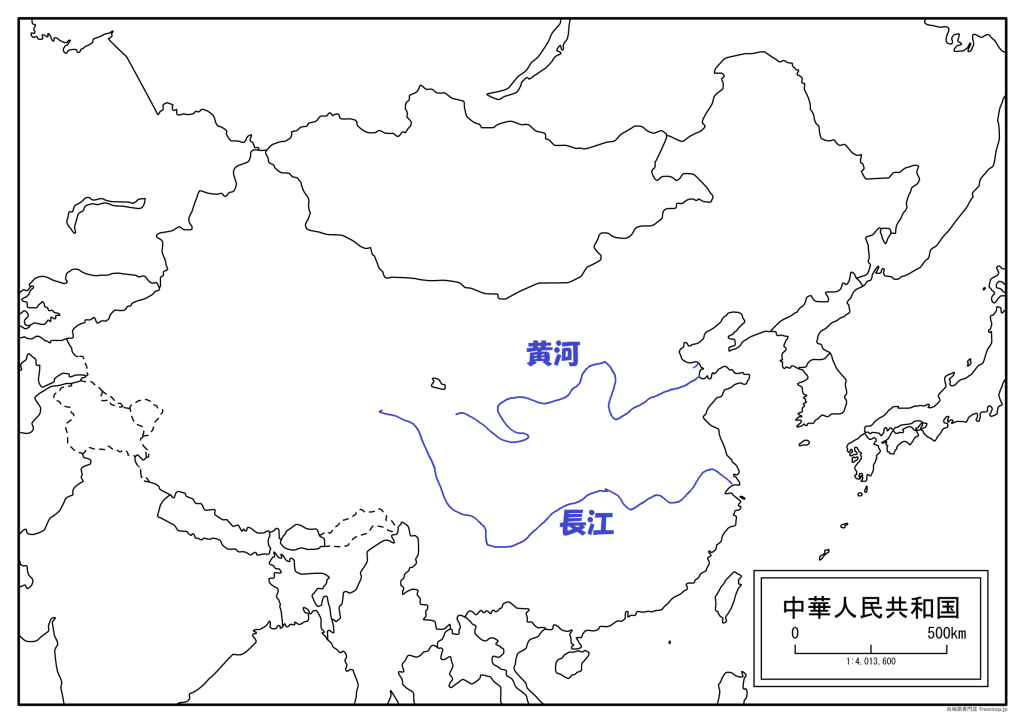
(出典:白地図専門店より改変 / CC-BY-4.0)
紀元前3000年頃には、黄河下流域、長江中・下流域などを中心に地域間の交流が始まり、政治的な統合が始まります。
紀元前1600年頃、黄河流域の都市を統合する形で、最古の王朝である殷が誕生しました。
殷では、「甲骨文字」が使われ、現在でも当時文字を刻まれた亀の甲羅等が残っています。

(出典:National Museum of China, CC BY-SA 3.0, via Wikimedia Commons)
B.C.1000年頃、殷に服属していた周が殷を倒したものの、その勢力は衰え、紀元前8世紀頃からは小さな国が乱立する戦国時代が続きました。
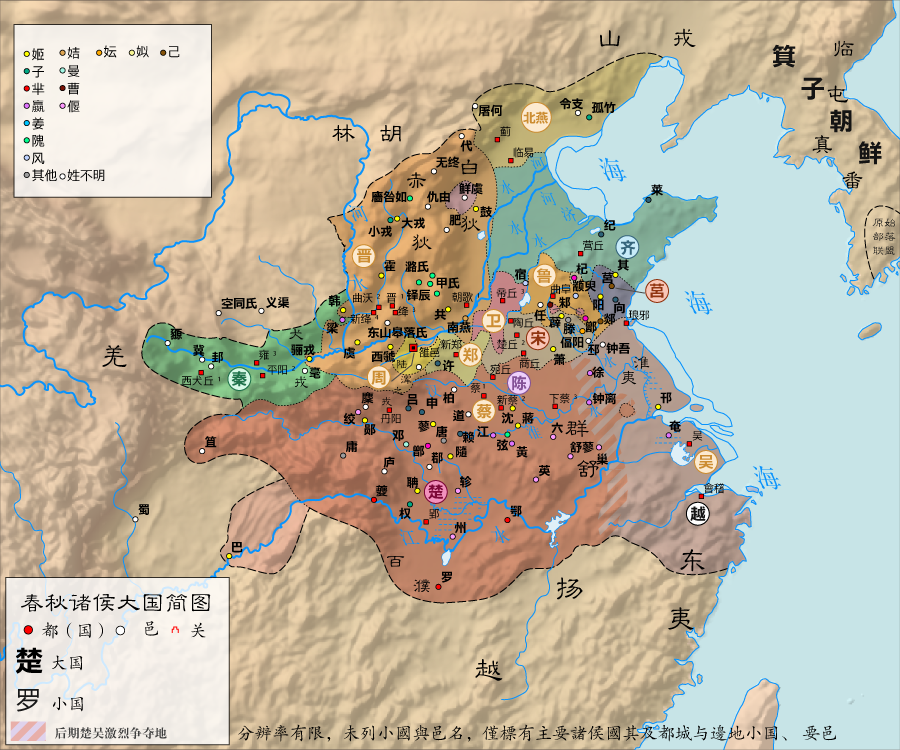
(出典:玖巧仔, CC BY-SA 3.0, via Wikimedia Commons)
紀元前3世紀に入ると、富国強兵をすすめる国々が周辺小国を併合し、戦国の七雄と呼ばれる7つの強国が台頭してきます。
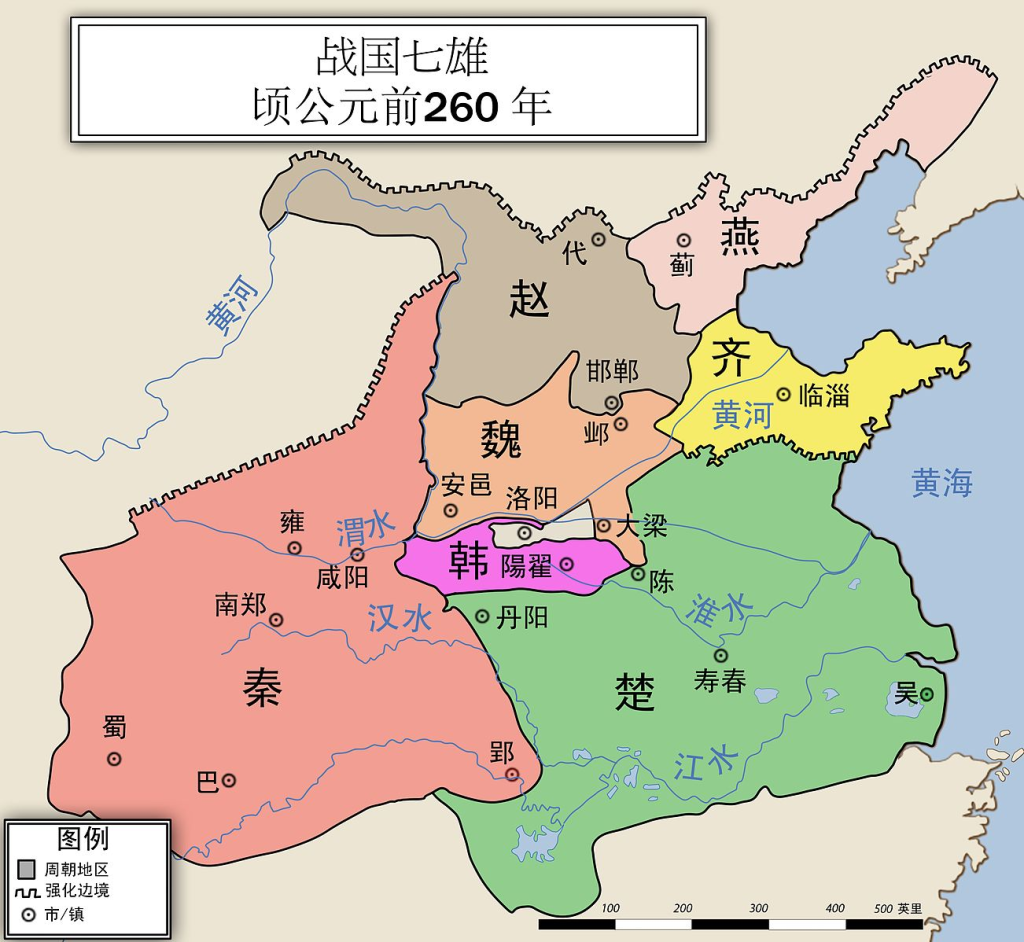
(出典:Philg88, CC BY 3.0, via Wikimedia Commons)
図4の西方に構える秦は、積極的な制度改革を行うことで国力をつけ、東方の6か国をつぎつぎに征服し、紀元前221年に中国を統一しました。
焚書により数学の資料が失われた
秦王である政(せい)は、始皇帝と名乗り、紀元前213年に焚書・坑儒という政策を行いました。

(出典:Unknown artistUnknown artist, Public domain, via Wikimedia Commons)
焚書では、医薬・占い・農業関係以外の書物をすべて焼き払うことで、思想統制を図りました。
また、秦より前の王朝に関連する書物を無かったことにすることで、中国の歴史の創始者であることをアピールする意味合いも含まれています。
焚書政策により、紀元前213年よりも前に書かれた主だった書籍が焼かれてしまい、秦以前の数学を知ることができなくなっています。
最古の数学書『周髀算經』『九章算術』
焚書政策で紀元前213年以前の本は焼かれてしまったため、中国数学を知る最古の手がかりとなっているのは、『周髀算經』と『九章算術』の2冊です。
天文学上の計算が中心の『周髀算經』
『周髀算經』は紀元前202年頃に書かれたと推測されていて、天文学に必要な計算を中心に解説しています。
その中でも有名なのが、ピタゴラスの定理の図による証明。
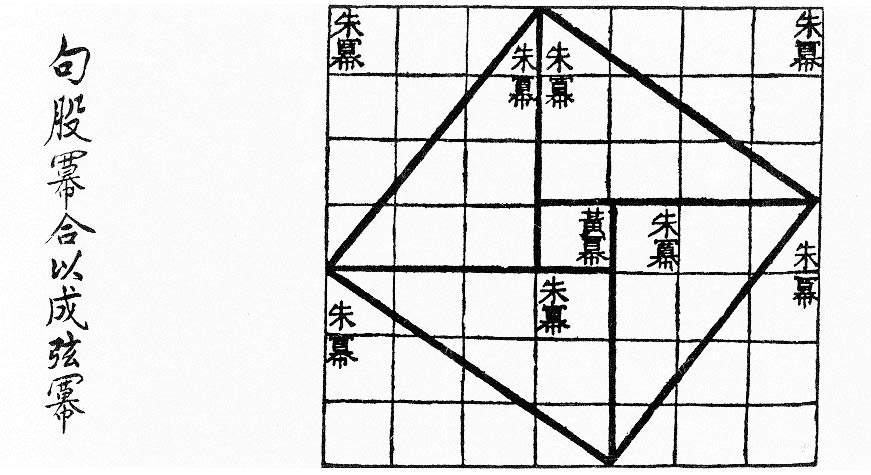
(出典:Wikipedia, Public domain)
円周率が$~3.14~$に近いことも述べられていて、同時代のギリシャの数学者ユークリッド(Euclid , B.C.330頃~B.C.275頃)の『原論』に含まれる内容も多数載っています。
中国数学の基礎となった『九章算術』
『周髀算經』と同じくらい古く、古代中国で最も影響力があったのは『九章算術』で、以下の9章から成っています。
- 方田(田畑の面積の計算等)
- 粟米(粟や米に関する比の問題等)
- 衰分(お金の分配や利息の問題等)
- 少広(土地の測量、平方根や立方根等)
- 商功(土木の計算等)
- 均輸(税の計算等)
- 盈不足(鶴亀算、仮置法等)
- 方程(一次方程式、連立方程式等)
- 句股(ピタゴラスの定理等)
合計246個の問題を扱い、網羅性に富んでいたことから、古代中国の中心的な数学書として扱われました。
紀元後263年には、魏の劉徽(りゅうき)が『九章算術』に解説を加え、西洋数学が入ってくる18世紀頃まで、中国数学に大きな影響を与え続けました。

(出典:See page for author, Public domain, via Wikimedia Commons)
遣唐使を通して日本にも輸入され、平安時代の日本の役人も『九章算術』から数学を学んだと考えられています。
まとめ・参考文献
紀元前の中国の歴史や最古の数学書について解説してきました。
- 秦の始皇帝の焚書政策によって、紀元前213年以前の数学書は存在しない。
- 最古の数学書は『周髀算經』と『九章算術』で、後の時代に大きな影響を与えた。
『周髀算經』と『九章算術』の詳しい内容については、【数学史5-4】以降で解説します。



秦の始皇帝はなぜ本を燃やしてしまったのだろう? もったいないなぁ。



中国の歴史は、自分から始まるように見せかけるためだよ。
以前の王朝の時代がわかるものは、すべて無かったことにしないといけないからね。



‥‥
参考文献(本の紹介ページにリンクしています)
- 『カッツ 数学の歴史』,pp.4-5
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.193-194
- 『数学史 数学5000年の歩み』,pp.135-137
- 『ずかん 数字』,pp.70-71
- 『数学の歴史物語』,pp.167-171
- 木村靖二・岸本美緒・小松久男(2022)『詳説 世界史 改訂版』,pp65-71,山川出版社.

コメント
コメント一覧 (2件)
古代中国の数学は紀元前186年の『算数書』と紀元前212年の岳麓書院蔵秦簡『数』があります.
「秦の始皇帝の焚書政策によって、紀元前213年以前の数学書は存在しない.」
この記述は誤りです.
宮田様
コメントありがとうございます。
自分の知識不足もあり、誤った表現となっていたところをご指摘いただき大変助かりました。
日本語の表現につきましては、今後も気を付けたいと思います。