紀元前に誕生し、中国数学の体系を完成させた『九章算術』。
この本の7章「盈不足」や8章「方程」では、一次方程式が扱われており、その中でも連立方程式の問題が中心となっています。
この記事では、『九章算術』に載っている連立方程式の解法を解説!
エジプトやバビロニアには無かった負の数の概念だけでなく、今で言う行列の知識まで使って様々な問題を解いています。
| 時代 | 紀元前2世紀頃 |
| 場所 | 中国 |
『九章算術』7章「盈不足」
『九章算術』は紀元前2世紀頃に書かれ、その後の中国数学を体系立てた数学書です。

(出典:See page for author, Public domain, via Wikimedia Commons)
全9章の中で、連立方程式を扱っているのは7章と8章であり、それぞれ違う解法が記されています。

「盈不足」は過不足算の考え方
7章「盈不足」の漢字を分解すると、「盈」と「不足」。
「盈」の訓読みは「盈(ちる)」(=「満ちる」)で、余っている様子を表す漢字であり、「不足」は足りない様子を表します。
この章で扱われていたのは、解を仮定したうえで実値との過不足から正しい解を導く方法。
バビロニアでも連立方程式の解法として、同様の方法が使われていたため、当時は基礎知識だったのかもしれません。

「盈不足」による連立方程式の解法
実際に『九章算術』に載っていた問題とその解法を見てみましょう。
今、善田は$~1~$畝で価は$~300~$銭、悪田は$~7~$畝で価は$~500~$銭である。今、合わせて$~1~$頃($~100~$畝)を買うと、価は$~1~$万銭であった。
善田と悪田の面積はそれぞれ何畝ずつか。
※「畝」は面積の単位で、$~1~$畝は約~100~$m2。「銭」は通貨の単位。
『九章算術』では、問題のすぐ下に答えと解説が載っています。
今回の問題の解説を、現代の数学記法で見てみましょう。
善田を$~20~$畝と仮定すれば、悪田は$~80~$畝となり、
\begin{align*}
20\cdot 300+80\cdot \frac{500}{7}&=6000+\frac{40000}{7} \\
\\
&=\frac{82000}{7} \\
\\
&=11714~\frac{2}{7}
\end{align*}で、$~1~$万銭よりも$~\displaystyle 1714\frac{2}{7}~$銭多くなる。
また、善田を$~10~$畝と仮定すれば、悪田は$~90~$畝となり、
\begin{align*}
10\cdot 300+90\cdot \frac{500}{7}&=3000+\frac{45000}{7} \\
\\
&=\frac{66000}{7} \\
\\
&=9428~\frac{4}{7}
\end{align*}で、$~1~$万銭よりも$~\displaystyle 571\frac{3}{7}~$銭不足する。
ここで、盈不足術にあてはめると、善田は
\begin{align*}
&~\frac{20\cdot 571\frac{3}{7}+10\cdot 1714\frac{2}{7}}{1714\frac{2}{7}+571\frac{3}{7}} \\
\\
&=\frac{20\cdot \frac{4000}{7}+10\cdot \frac{12000}{7}}{\frac{12000}{7}+\frac{4000}{7}} \\
\\
&=\frac{80000+120000}{12000+4000} \\
\\
&=\frac{200}{16} \\
\\
&=12~\frac{1}{2}~~~~(畝)
\end{align*}と求まり、悪田は、
\begin{align*}
&~\frac{80\cdot 571\frac{3}{7}+90\cdot 1714\frac{2}{7}}{1714\frac{2}{7}+571\frac{3}{7}} \\
\\
&=\frac{80\cdot \frac{4000}{7}+90\cdot \frac{12000}{7}}{\frac{12000}{7}+\frac{4000}{7}} \\
\\
&=\frac{320000+1080000}{12000+4000} \\
\\
&=\frac{1400}{16} \\
\\
&=87~\frac{1}{2}~~~~(畝)
\end{align*}と求まった。
ここで使っている「盈不足術」とは、『九章算術』7章の最初に載っている公式です。
求めたい数量に対して、$~a~$と仮定すると$~m~$多く、$~b~$と仮定すると$~n~$不足するとき、その数量は
\frac{an+bm}{m+n}で表せる。
先ほどの第17問に関しては、善田を求めるために、
a=10~,~ m=1714~\frac{2}{7}~,~b=20~,~n=\displaystyle 571~\frac{3}{7}を代入し、悪田を求めるために、
a=80~,~ m=1714~\frac{2}{7}~,~b=90~,~n=\displaystyle 571~\frac{3}{7}を代入しています。
『九章算術』8章「方程」
8章は「方程」とあるものの、最も基本的な1文字の方程式は扱っていません。
この章では、2文字以上の連立方程式を、「盈不足」とは違った解法で解いています。
行列の考え方で連立方程式を解いた
驚くべきことに、8章で連立方程式を解くために使っていたのは、行列の掃き出し法の考え方。
8章の最初の問題で、その解き方を見てみましょう。
今、上禾※1が$~3~$束、中禾が$~2~$束、下禾が$~1~$束で実が$~39~$斗※2になり、上禾が$~2~$束、中禾が$~3~$束、下禾が$~1~$束で実が$~34~$斗になり、上禾が$~1~$束、中禾が$~2~$束、下禾が$~3~$束で実が$~26~$斗になる。
上禾・中禾・下禾の$~1~$束あたりの実は、それぞれいくらになるか。
※1「禾」は粟物の総称で、上禾は入っている実が多く、下禾は実が少ない。
※2「斗」は尺貫法における体積の単位。1斗は約18L。
$~1~$束あたりの実の数を、上禾は$~x~$斗、中禾は$~y~$斗、下禾は$~z~$斗とすると、次のような連立方程式ができます。
\begin{cases}
3x+2y+z=39&\\
2x+3y+z=34& \\
x+2y+3z=26&
\end{cases}この連立方程式を、『九章算術』では以下のような説明に従って解きます。
方程術に従い、上禾$~3~$束、中禾$~2~$束、下禾$~1~$束、実$~39~$斗を右列に置く。
中列・左列についても右列と同様に置く。
右列の上禾をすべて中列にかけて、右列からただちに引く。
その次に、右列の上禾をすべて左列にかけて、右列でただちに引く。
その後、中列の中禾の残りをすべて左列にかけて、中列でただちに引く。
左列に残りがあれば、上を法とし、下を実とする。この実が下禾の実となる。
中禾を求めるには、法を中列の下の実にかけて、それから下禾の実を引く。
残りを中禾の束数で割ると、中禾の実である。
上禾を求めるには、法を右列の下の実にかけて、これから下禾と中禾の実を引く。
残りの$~111~$を上禾の束数で割ると、上禾の実となる。
三者とも実を法で割ると、上・中・下禾それぞれの実の斗数が求まる。
この説明を今の行列で考えてみましょう。
方程術に従い、上禾$~3~$束、中禾$~2~$束、下禾$~1~$束、実$~39~$斗を右列に置く。
中列(上禾$~2~$束、中禾$~3~$束、下禾$~1~$束、実$~34~$斗)・左列(上禾$~1~$束、中禾$~2~$束、下禾$~3~$束、実$~26~$斗)についても右列と同様に置く。
\begin{pmatrix}
1 & 2 & 3 \\
2 & 3 & 2 \\
3 & 1 & 1 \\
26 & 34 & 39
\end{pmatrix}右列の上禾($~3~$)をすべて中列にかけて、右列からただちに引く(中列の1行目が$~0~$になるまで引く)
\begin{pmatrix}
1 & 6 & 3 \\
2 & 9 & 2 \\
3 & 3 & 1 \\
26 & 102 & 39
\end{pmatrix}
\xrightarrow{1回目}
\begin{pmatrix}
1 & 3 & 3 \\
2 & 7 & 2 \\
3 & 2 & 1 \\
26 & 63 & 39
\end{pmatrix}
\xrightarrow{2回目}
\begin{pmatrix}
1 & 0 & 3 \\
2 & 5 & 2 \\
3 & 1 & 1 \\
26 & 24 & 39
\end{pmatrix}その次に、右列の上禾($~3~$)をすべて左列にかけて、右列でただちに引く。(左列の1行目が$~0~$になるまで引く)
\begin{pmatrix}
3 & 0 & 3 \\
6 & 5 & 2 \\
9 & 1 & 1 \\
78 & 24 & 39
\end{pmatrix}
\xrightarrow{1回目}
\begin{pmatrix}
0 & 0 & 3 \\
4 & 5 & 2 \\
8 & 1 & 1 \\
39 & 24 & 39
\end{pmatrix}その後、中列の中禾($~5~$)の残りをすべて左列にかけて、中列でただちに引く。
\begin{pmatrix}
0 & 0 & 3 \\
20 & 5 & 2 \\
40 & 1 & 1 \\
195 & 24 & 39
\end{pmatrix}
\xrightarrow{1回目}
\begin{pmatrix}
0 & 0 & 3 \\
15 & 5 & 2 \\
39 & 1 & 1 \\
171 & 24 & 39
\end{pmatrix}
\cdots
\xrightarrow{4回目}
\begin{pmatrix}
0 & 0 & 3 \\
0 & 5 & 2 \\
36 & 1 & 1 \\
99 & 24 & 39
\end{pmatrix}左列に残りがあれば、(最大公約数である$~9~$でわったうえで、)上($~4~$)を法とし、下($~11~$)を実とする。
\begin{pmatrix}
0 & 0 & 3 \\
0 & 5 & 2 \\
36 & 1 & 1 \\
99 & 24 & 39
\end{pmatrix}
=
\begin{pmatrix}
0 & 0 & 3 \\
0 & 5 & 2 \\
4 & 1 & 1 \\
11 & 24 & 39
\end{pmatrix}
\xrightarrow{法を4として}
\begin{pmatrix}
0 & 0 & 3 \\
0 & 5 & 2 \\
1 & 1 & 1 \\
11 & 24 & 39
\end{pmatrix}
この実が下禾の実($~11~$)となる。
中禾を求めるには、法($~4~$)を中列の下($~24~$)の実にかけて、それから下禾の実($~11~$)を引く。
4\times 24-11=85
残りを中禾の束数($~5~$)で割ると、中禾の実($~17~$)である。
85\div 5=17
上禾を求めるには、法($~4~$)を右列の下の実($~39~$)にかけて、これから下禾の実($~11~$)と中禾の実($~17~$)を引く。(右列の2行目より、中禾の実は2回引く)
4 \times 39-11-17-17=111
残りの$~111~$を上禾の束数($~3~$)で割ると、上禾の実($~37~$)となる。
111 \div 3=37
三者とも実(上禾$~37~$、中禾$~17~$、下禾$~11~$)を法($~4~$)で割ると、上・中・下禾それぞれの実の斗数が求まる。
\begin{cases}
&上禾=\displaystyle \frac{37}{4}=9\frac{1}{4} 斗 \\
\\
&中禾=\displaystyle \frac{17}{4}=4\frac{1}{4} 斗\\
\\
&下禾=\displaystyle \frac{11}{4}=2\frac{3}{4} 斗 \\
\end{cases} 最後は行列の操作ではなく、行列から式を作って計算しています。
単なる四則計算の組み合わせとして見た方が、算木という計算道具がある以上、素早く計算できたのでしょう。

ちなみに、かっこを使って行列を表す代わりに、表を用いて連立方程式を解いていました。
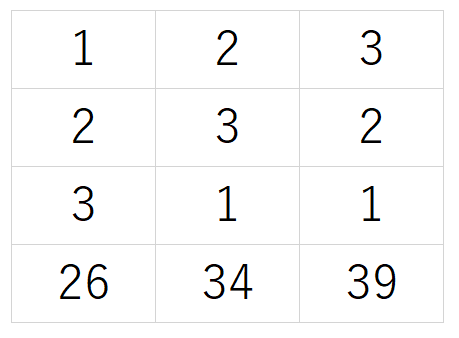
負の数が途中式で登場する
『九章算術』8章第1問でもあったように、『九章算術』では実生活に基づいた数値が用いられています。
そのため、問題文や答えに負の数が登場することは無かったものの、途中式で負の数が必要となる問題がいくつかあります。
最初に負の数が登場するのは、以下の問題です。
今、上禾※3が$~2~$束、中禾が$~3~$束、下禾が$~4~$束あって、実はすべて$~1~$斗※4に満たない。
上禾は中禾を、中禾は下禾を、下禾は上禾をそれぞれ$~1~$束取れば実は$~1~$斗に達する。
上禾・中禾・下禾の$~1~$束あたりの実は、それぞれいくらになるか。
※3「禾」は粟物の総称で、上禾は入っている実が多く、下禾は実が少ない。
※4「斗」は尺貫法における体積の単位。1斗は約18L。
$~1~$束あたりの実の数を、上禾は$~x~$斗、中禾は$~y~$斗、下禾は$~z~$斗とすると、次のような連立方程式ができます。
\begin{cases}
2x+y=1& \\
3y+z=1& \\
x+4z=1&
\end{cases}この連立方程式を、『九章算術』8章第1問のように方程術(行列の掃き出し法)を使って解くと、以下のように負の数が過程で登場します。
\begin{align*}
\begin{pmatrix}
1 & 0 & 2 \\
0 & 3 & 1 \\
4 & 1 & 0 \\
1 & 1 & 1
\end{pmatrix}
&\xrightarrow{左列を2倍}
\begin{pmatrix}
2 & 0 & 2 \\
0 & 3 & 1 \\
8 & 1 & 0 \\
2 & 1 & 1
\end{pmatrix}
\\
&\xrightarrow{左列から右列をひく}
\begin{pmatrix}
0 & 0 & 2 \\
-1 & 3 & 1 \\
8 & 1 & 0 \\
1 & 1 & 1
\end{pmatrix}
\\
&\xrightarrow{左列を3倍}
\begin{pmatrix}
0 & 0 & 2 \\
-3 & 3 & 1 \\
24 & 1 & 0 \\
3 & 1 & 1
\end{pmatrix}
\\
&\xrightarrow{左列に中列をたす}
\begin{pmatrix}
0 & 0 & 2 \\
0 & 3 & 1 \\
25 & 1 & 0 \\
4 & 1 & 1
\end{pmatrix}
\\
&\xrightarrow{法を25として}
\begin{pmatrix}
0 & 0 & 2 \\
0 & 3 & 1 \\
1 & 1 & 0 \\
4 & 1 & 1
\end{pmatrix}
\end{align*}以上のような変形から、答えは
上禾=\frac{9}{25}斗~,~中禾=\frac{7}{25}斗~,下禾=\frac{4}{25}斗となるため、あくまでも負の数が登場するのは途中式のみです。
負の数の扱い方の説明は、『九章算術』のこの『九章算術』8章第3問の解説の中に載っていました。
正負術に関して、ひき算については同符号の$~2~$数は互いに引き、異符号の$~2~$数は互いに加える。
$~0~$から正を引けばこれを負とし、$~0~$から負を引けばこれを正とする。
たし算については異符号の$~2~$数は互いに引き、同符号の$~2~$数は互いに加える。
$~0~$に正を加えればこれを正とし、$~0~$に負を加えればこれを負とする。
この「正負術」を具体例を通して見てみましょう。
ひき算については同符号の$~2~$数は互いに引き、異符号の$~2~$数は互いに加える。
\begin{align*}
(-6)-(-4)&=-(6-4)=-2 \\
(-6)-(+2)&=-(6+2)=-8
\end{align*}$~0~$から正を引けばこれを負とし、$~0~$から負を引けばこれを正とする。
\begin{align*}
0-(+4)&=-4 \\
0-(-4)&=+4
\end{align*}たし算については異符号の$~2~$数は互いに引き、同符号の$~2~$数は互いに加える。
\begin{align*}
(-6)+(+4)&=-(6-4)=-2 \\
(-6)+(-2)&=-(6+2)=-8
\end{align*}$~0~$に正を加えればこれを正とし、$~0~$に負を加えればこれを負とする。
\begin{align*}
0+(+4)&=+4 \\
0+(-4)&=-4
\end{align*}中学1年生の「正負の数」で学ぶ加法・減法を説明していることがわかるでしょう。
『九章算術』のこの一節は、負の数の概念について言及した世界最古の文献となっています。
まとめ・参考文献
古代中国における方程式、とりわけ連立方程式の解法について解説してきました。
- 「盈不足」では解を仮定したうえで、実値との差から正しい解を調整した。
- 「方程術」では行列の掃き出し法を使って、3文字以上の連立方程式を解いた。
- 方程式を解く中で負の数が登場し、その扱い方が『九章算術』で説明されている。
行列や負の数を初めて使用した古代中国。
次の記事では、古代中国の円について解説します。



3文字の連立方程式を機械的に解く方法を見つけていたっていう事実がすごいね。



算木により、計算力が高かった中国人だからこそなせる解法だよね。
参考文献(本の紹介ページにリンクしています)
- 『カッツ 数学の歴史』,p.20-24
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.194-195
- 『数学史 数学5000年の歩み』,pp.135-137
- 『ずかん 数字』,pp.70-77
- 『数学の歴史物語』,pp.167-183
- 馬場理恵子「『九章算術』訳注稿(21)」,<http://pal.las.osaka-sandai.ac.jp/~suanshu/articles/9Chapters21.pdf>
- 吉村昌之「『九章算術』訳注稿(24)」,<https://osu.repo.nii.ac.jp/?action=repository_uri&item_id=1854&file_id=22&file_no=1>
- 張替俊夫「『九章算術』訳注稿(25)」,< https://osu.repo.nii.ac.jp/?action=repository_action_common_download&item_id=1931&item_no=1&attribute_id=22&file_no=1 >

コメント