四大文明の一つで長い歴史を持つ中国。
しかし、紀元前213年の焚書政策により、紀元前の数学関係の資料はほとんど失われてしまいました。
そのため、古代中国の数学を知るための資料は、紀元前2世紀頃に書かれたとされる『周髀算經』と『九章算術』に代表されます。
この記事では、『九章算術』に載っているものを中心に、古代中国の数学の特徴を大まかに解説。
長い歴史を踏まえながら、当時の中国の数学を見ていきましょう。
- 古代中国の数学史の流れ
- 古代中国の数学の内容
| 時代 | B.C.6000年頃~263年 |
| 場所 | 中国 |
古代中国の数学史年表
中国は紀元前6000年からの長い歴史を持つものの、数学史としてはエジプトやバビロニアよりも浅いです。
黄河や長江流域で中国文明が興る。
黄河流域ではアワ、長江流域では稲が中心の農耕が始まる。
数百人規模の村落が生まれる。
人工的な水田や土器を作り、集団での生活が行われるようになった。
村落どうしの交流・争いが始まる。
各地域で政治的統合がなされていった。
殷が倒されることにより、戦国時代に突入する。
周が殷を倒したことにより、小さな国が乱立する戦国時代に突入した。
秦が中国統一。
約800年間の戦国時代が幕を閉じた。
秦の始皇帝が焚書政策を行う。
数学関係の書物はすべて焼き払われた。
『周髀算經』が記される。
天文学に必要な計算が中心ではあるものの、古代中国の数学を知る貴重な資料となっている。
『九章算術』が記される。
古代中国の数学を体系立てた数学書で、分野ごとに問題がまとめられている。
劉徽が『九章算術』に注釈を加える。
解法に証明を与えることで、より洗練された内容となった。
祖冲之が$~\pi~$の近似値として、$~\displaystyle \frac{355}{113}~$を与える。
劉徽の考え方を延長することで、小数第7位まで正確に求めた。
以上のように、数学のことがわかる最古の資料は、紀元前202年の『周髀算經』になります。
古代中国の数学の内容
紀元前213年の焚書政策により、それ以前の数学史料は一切残っていません。
しかし、紀元前202年頃の『周髀算經』、それと同時期の『九章算術』により、古代中国の数学体系が確立しました。

数字は甲骨文字による合字
現在我々が使っている漢字の祖先は甲骨文字であり、紀元前1600年頃の殷の時代から使われ始めました。
甲骨文字には、13種類の数字が用意されています。
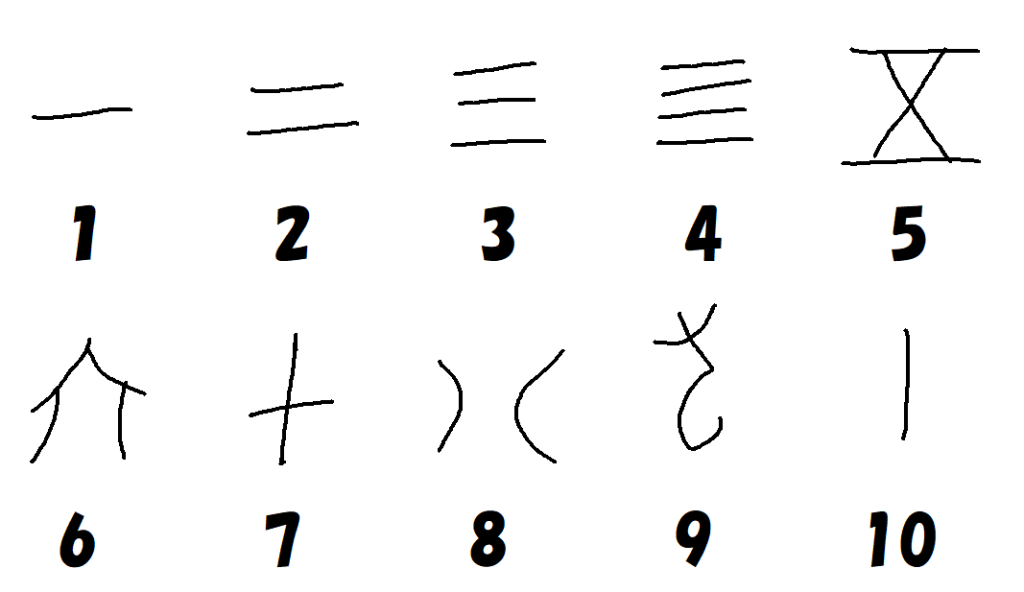
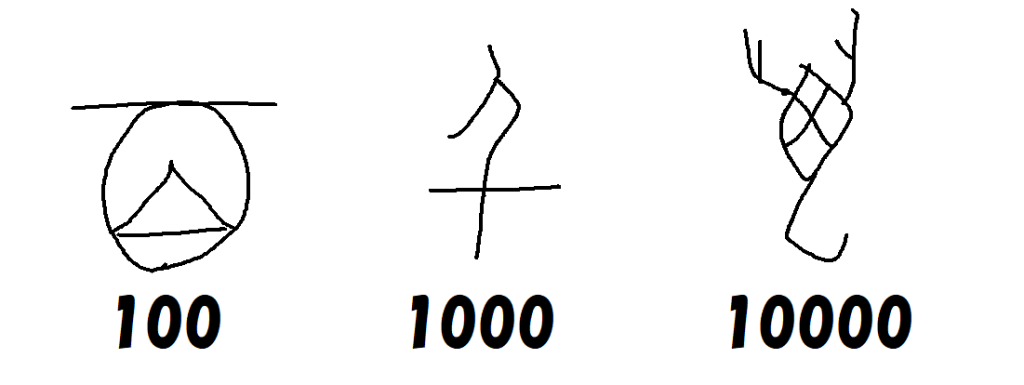
これら以外の数字については、2つ以上の数字を組み合わせて新しい数字を作る、合字の考え方で表されました。
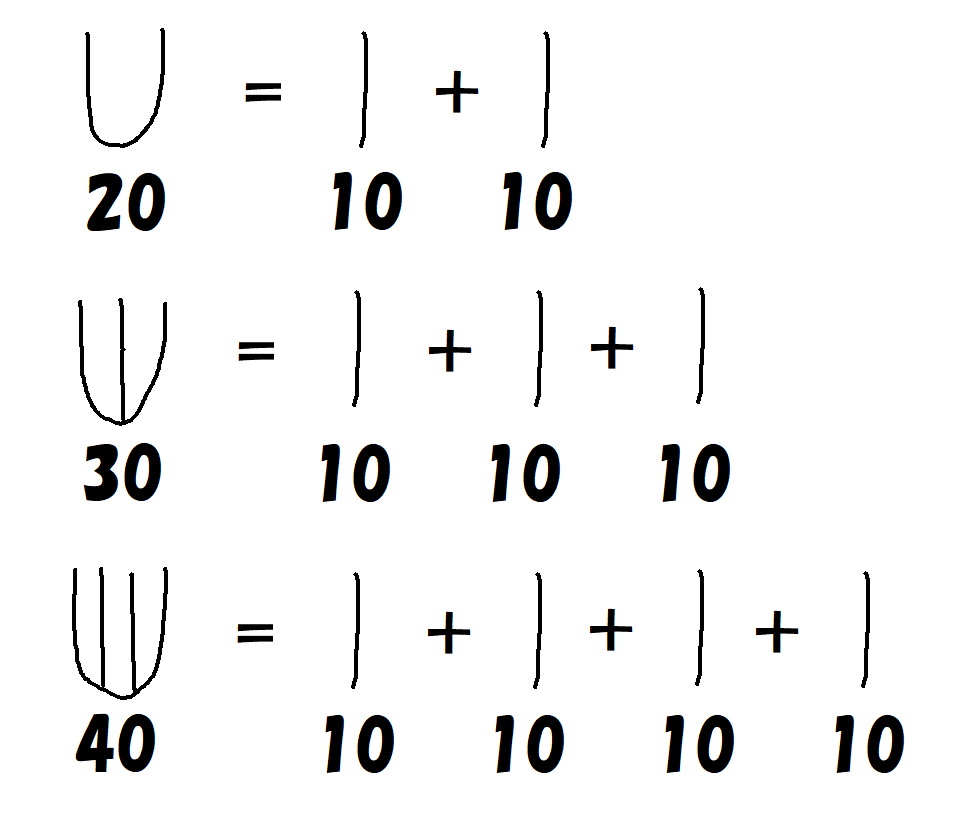

合字の作り方として、たし算とかけ算が混ざっているのも甲骨文字の数字の特徴となっています。

計算手段は算木
古代中国では、そろばんの祖先にあたる「算木」という道具で計算を行っていました。
数字の表し方は横式と縦式があり、これらを位ごとに交互に使用し、数の読み間違いを防いでいました。
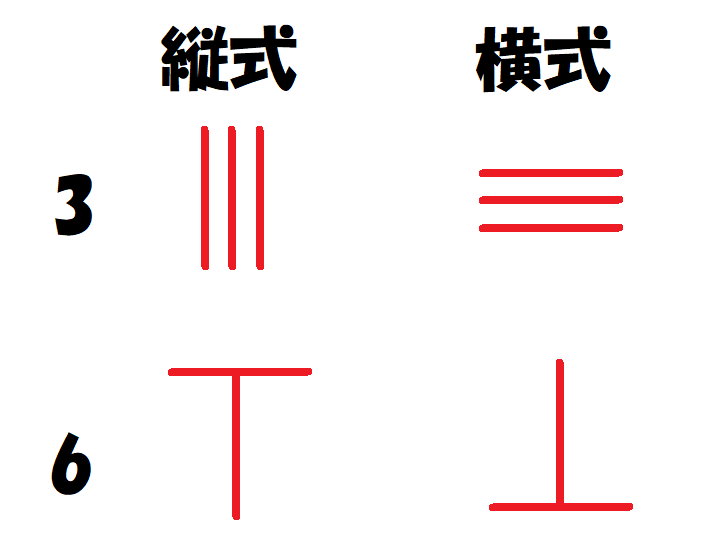
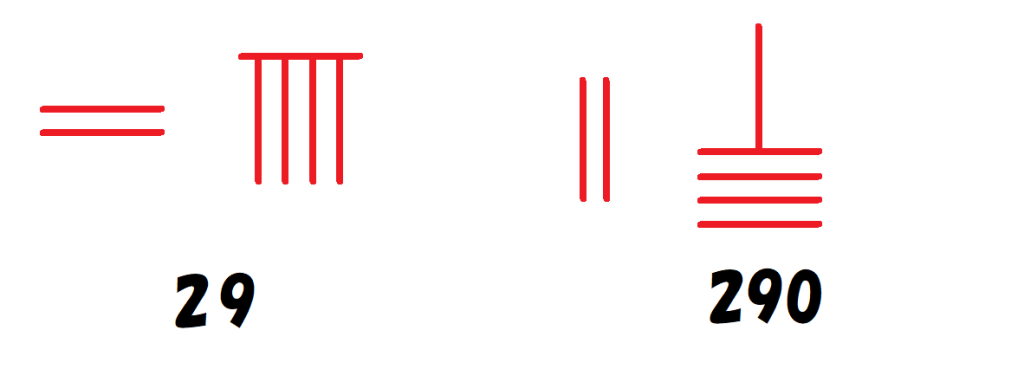
さらに赤い算木(正の数)と黒い算木(負の数)が用意されており、世界で初めて負の数を計算で使っていました。
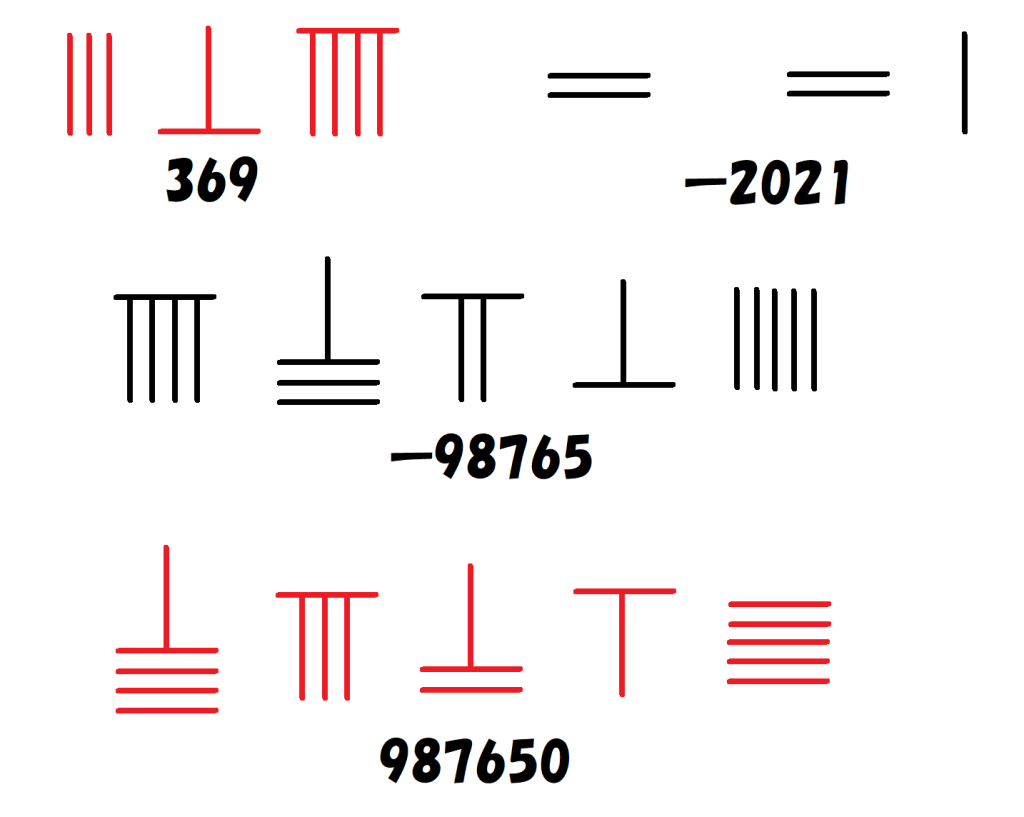
算木を使うことで、かけ算でさえもものすごいスピードで行われていたことがわかっています。

連立方程式を行列で解いた
『九章算術』の中では、連立方程式の解法として、行列の掃き出し法と同様の方法が紹介されていました。
『九章算術』8章第1問に出てくる連立方程式
\begin{cases}
3x+2y+z=39&\\
2x+3y+z=34& \\
x+2y+3z=26&
\end{cases}を例にすると、各係数を縦に並べることで、
\begin{pmatrix}
1 & 2 & 3 \\
2 & 3 & 2 \\
3 & 1 & 1 \\
26 & 34 & 39
\end{pmatrix}という行列(表)を作成します。
この行列を、以下のように変形していきました。
\begin{align*}
&~\begin{pmatrix}
1 & 2 & 3 \\
2 & 3 & 2 \\
3 & 1 & 1 \\
26 & 34 & 39
\end{pmatrix}
\\
\xrightarrow{中列を3倍}&
\begin{pmatrix}
1 & 6 & 3 \\
2 & 9 & 2 \\
3 & 3 & 1 \\
26 & 102 & 39
\end{pmatrix}
\\
\xrightarrow{右列の2倍で中列をひく}&
\begin{pmatrix}
1 & 0 & 3 \\
2 & 5 & 2 \\
3 & 1 & 1 \\
26 & 24 & 39
\end{pmatrix}
\\
\xrightarrow{左列を3倍}&
\begin{pmatrix}
3 & 0 & 3 \\
6 & 5 & 2 \\
9 & 1 & 1 \\
78 & 24 & 39
\end{pmatrix}
\\
\xrightarrow{右列で左列をひく}&
\begin{pmatrix}
0 & 0 & 3 \\
4 & 5 & 2 \\
8 & 1 & 1 \\
39 & 24 & 39
\end{pmatrix}
\\
\xrightarrow{左列を5倍}&
\begin{pmatrix}
0 & 0 & 3 \\
20 & 5 & 2 \\
40 & 1 & 1 \\
195 & 24 & 39
\end{pmatrix}
\\
\xrightarrow{中列の4倍で左列をひく}&
\begin{pmatrix}
0 & 0 & 3 \\
0 & 5 & 2 \\
36 & 1 & 1 \\
99 & 24 & 39
\end{pmatrix}
\\
\xrightarrow{中列の4倍で左列をひく}&
\begin{pmatrix}
0 & 0 & 3 \\
0 & 5 & 2 \\
36 & 1 & 1 \\
99 & 24 & 39
\end{pmatrix}
\\
\xrightarrow{左列を9で割る}&
\begin{pmatrix}
0 & 0 & 3 \\
0 & 5 & 2 \\
4 & 1 & 1 \\
11 & 24 & 39
\end{pmatrix}
\end{align*}変形後の行列から、$~z=\displaystyle \frac{11}{4}~$とわかり、中列から$~y~$、右列から$~x~$と順に求まります。
負の数が途中の行列で出てきたり、4文字以上の連立方程式となったりする問題も『九章算術』には登場し、連立方程式のレベルの高さがわかります。

円周率は3
『九章算術』における円周率は$~3~$であり、以下の問題がその根拠となっています。
今、円周$~30~$歩※1、直径$~10~$歩の円田がある。
田の面積はどのくらいか。
※1「歩」は周(B.C.11世紀頃~B.C.256)に定められた長さの単位で、当時は1歩=約1.38m。
円周率を$~3~$にすることで、計算上非常に便利であり、その点を第一に考えていました。
円の面積を求める公式も、半径ではなく直径や円周といった実測可能な長さを使ったものが4つ与えられており、ここからも実用性を重んじていることがわかります。
円周を$~\ell~$、円の直径を$~d~$、円の面積を$~S~$とする。
① $~\displaystyle S=\frac{\ell}{2}\cdot \frac{d}{2}~$
② $~\displaystyle S=\frac{\ell \cdot d}{4}~$
③ $~\displaystyle S=\frac{d^2 \cdot 3}{4}~$
④ $~\displaystyle S=\frac{\ell^2}{12}~$

有限専用の開平法があった
『九章算術』において、根が有限な数となるとき専用の開平法が紹介されていました。
その方法とは、正方形の面積から1辺の長さを出すことを考え、正方形を分割していくという幾何的なアプローチです。
『九章算術』4章第12問で登場する、$~55225~$の平方根を考えるときには、図8のような正方形を考えました。
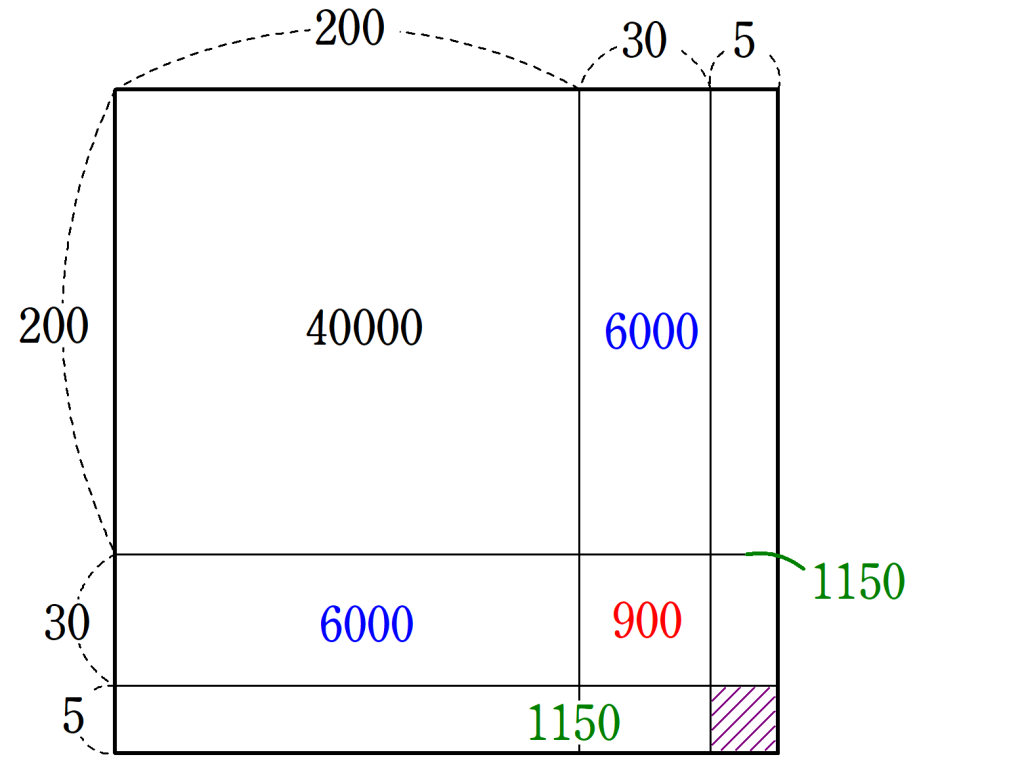
図8を使って、面積が$~55225~$を超えないように一辺の長さを求めていくと、$~235~$が求まります。
そのため、$~2~$の平方根のような無理数を扱うことはできませんでした。

三平方の定理も術として解いた
今で言う「三平方の定理」は、『九章算術』において「句股の術」として知られていました。
句・股をそれぞれ自乗※1して、それらを足して開平術を使えば、弦の長さが求まる。
股を自乗して、弦の自乗したものから引き、その余りに開平術を使えば、句の長さが求まる。
句を自乗して、弦の自乗したものから引き、その余りに開平術を使えば、股の長さが求まる。
この「句股の術」を使うことで、図9のような基本的な問題が簡単に解けました。
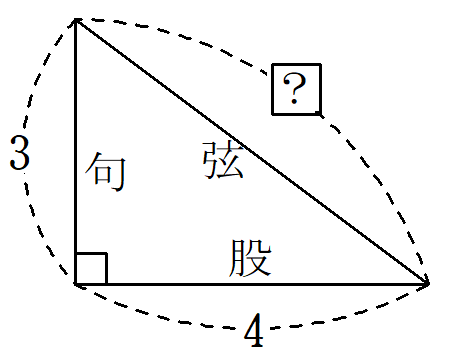
『九章算術』ではこのような基本問題だけでなく、長めの文章題まで紹介されており、各問題に応じた計算術(公式)が用意されていました。
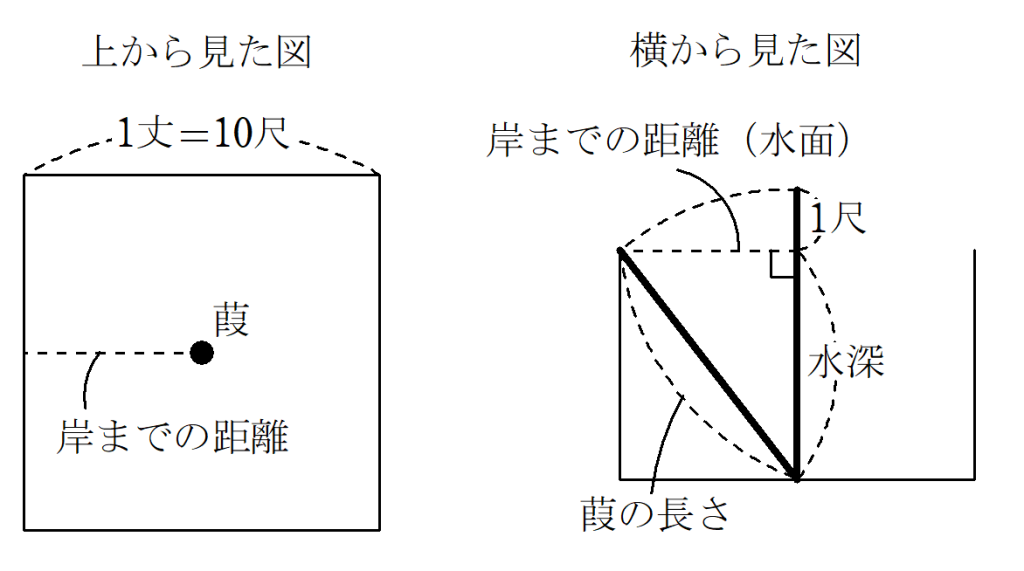
例として、池の中央に生えている葭の長さを求める問題(図10)に関しては、
(葭の長さ)=\frac{(岸までの距離)^2-1^2}{2 \times 1}+1
という専用術で求まります。
三平方の定理の文章題といっても、ほとんどの問題は二次方程式を使わないという点も『九章算術』の特徴です。

二次方程式を特殊な開平法で解いた
『九章算術』において、$~x^2-3x+2=0~$のように、$~x~$の係数が$~0~$でない二次方程式は2題だけ登場します。
その2題については、「帯従開平」という特殊な開平法を使って解きました。
『九章算術』9章第11問を解く上で出てくる二次方程式$~x^2+68x-2688=0~$については、以下のように求められました。
\begin{align*}
x&=(\sqrt{2688\times 4+68^2}-68) \div 2 \\
&=(\sqrt{15376}-68) \div 2 \\
&=(124-68) \div 2 \\
&=28
\end{align*}実はこの式、現在の解の公式における$~a=1~$かつ負の解が出ないパターンとなっており、263年には劉徽が幾何的に証明しました。

まとめ・参考文献
古代中国の数学について概説してきました。
- 数字は甲骨文字、計算では算木が使われた。
- 紀元前2世紀頃の『九章算術』に、古代中国数学の知識がまとめられている。
- 行列の掃き出し法や二次方程式の解の公式の利用など、高度な数学的知識が垣間見える。
紀元前213年の焚書政策という歴史を持ちながらも、『九章算術』をもとに中国の数学は発展していきました。
『九章算術』の内容は遣隋使や遣唐使などによって日本に伝わり、和算に少なからず影響を与えています。

秦の始皇帝がいなければ、もっと数学が発展していたかもしれないね!



始皇帝以前の資料がほとんど発見されていないことを考えると、彼の焚書政策への徹底ぶりのすごさがわかるね‥‥。


コメント
コメント一覧 (2件)
岳麓院蔵秦簡『数』訳注 紀元前212年(始皇帝35年)
『張家山漢簡<<算数書>>』紀元前186年成立
詳細は「古代中国古算書研究会」にアクセスしてください.
古代中国数学史・和算研究者です.
宮田様
コメントありがとうございます。
『数』や『算数書』という書簡については、存在を初めて知りました。
自分が持っている本以外からも情報を仕入れていかないと、正確な情報の提供は難しいですね。
ご指摘いただき、大変助かりました。