四大文明の1つとして有名なエジプト文明。
そこで興った古代エジプトの数学は、パピルスという巻物だけでなく、ピラミッドという具体物によって現代にまで伝わっています。
この記事では、古代エジプトの数学が発展していく様子を年表形式でまとめるとともに、その内容を解説。
約1万年前から始まったエジプト文明の長い歴史の中から、数学関連の話題を拾い上げてみましょう。
- 古代エジプトの数学史の流れ
- 古代エジプトの数学の内容
| 時代 | B.C.5000年頃~B.C.30年頃 |
| 場所 | エジプト |
古代エジプトの数学史年表
歴史学上は古代エジプトを、紀元前3000年頃~紀元前332年と定義するようですが、この年表ではエジプト文明の興りまでさかのぼっています。
クフ王のピラミッドが建設される。
古代エジプト期の終了。
古代エジプトの数学の内容
『リンド・パピルス』や『モスクワ・パピルス』からわかる、古代エジプトの数学の内容や特徴について、解説していきます。
実用的な面を重視した
古代エジプトの数学の最たる特徴は、実生活に即した内容を扱っているということです。
エジプト文明の勃興に寄与したナイル川は、毎年氾濫し、川沿いの集落を飲み込んでいました。
そのため、土地(geo)の測量(metry)を毎年行う必要があり、幾何学(geometry)を中心とする実用的な数学が必要とされたのです。

実際、『リンド・パピルス』には土地の面積を求める問題をはじめ、パンを分ける問題、穀物の量を求める問題などが収録されています。
数字は象形文字
エジプト文明では、紀元前4000年頃から象形文字が使われています。
その中でも、神殿や石碑に刻むためのヒエログリフ、パピルスに書きこむためのヒエラティックの2種類が並行して使われ、数字についてもそれぞれで用意されていました。
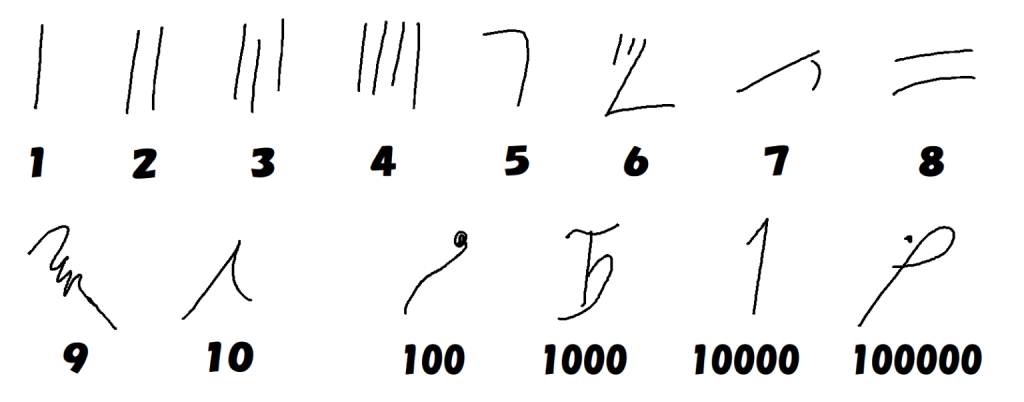
ヒエログリフは絵に最も近い文字で、$~10~$のべき乗ごとに用意された7種類の数字をひたすら並べて表します。
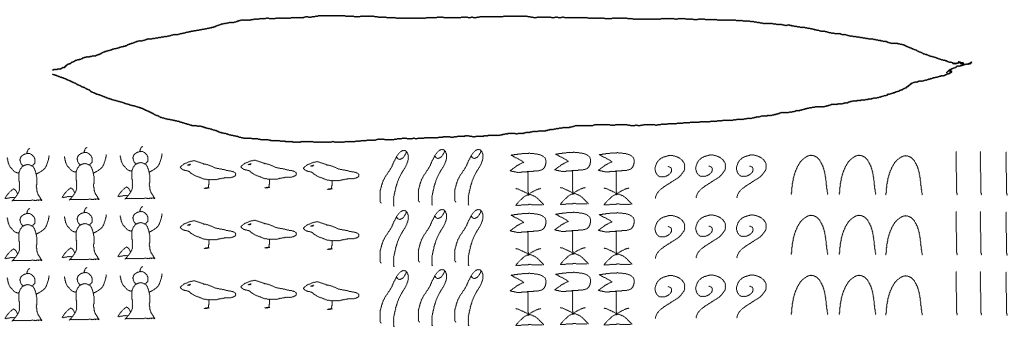
ヒエラティックについては、ヒエログリフを簡素化したもので、$~5~$から$~9~$は縦棒を並べる必要がなくなりました。

四則計算を効率的に行った
必要な数だけ数字を書き並べるという表記方法であったため、たし算・ひき算については単純に行われていました。
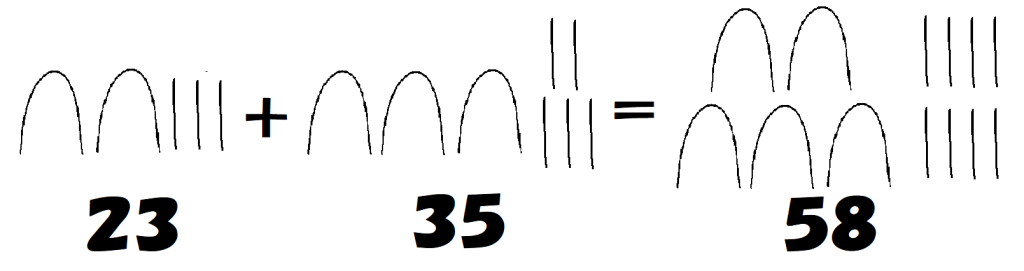
かけ算については、たし算に直して計算する必要がありましたが、その中で「2倍法」を活用して、計算を効率的に行いました。
$~15 \times 10~$を計算する。
まず、$~15 \times (2~のベキ乗)~$のリストを作る。(かける数が$~10~$を超える手前まで)
\begin{align*}
15 \times 1&=15~~~~~\cdots ① \\
15 \times 2&=30~~~~~\cdots ② \\
15 \times 4&=60~~~~~\cdots ③ \\
15 \times 8&=120~~~~~\cdots ④ \\
\end{align*}次に、$~10~$を$~2~$のベキ乗の和で表すと、
10=8+2
なので、$~④+②~$より、
\begin{align*}
15 \times (8+2)&=120+30 \\
15 \times 10&=150
\end{align*}と求まる。
わり算も$~2~$のベキ乗のリストを利用して、効率的に行っています。

分数は単位分数が中心
古代エジプトの分数は、分子が$~1~$である単位分数と$~\displaystyle \frac{2}{3}~$のみが用意されていました。
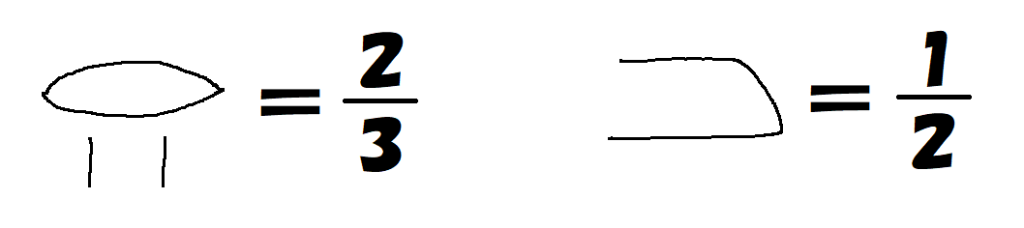
単位分数が好まれた理由は、実生活で役に立つからです。
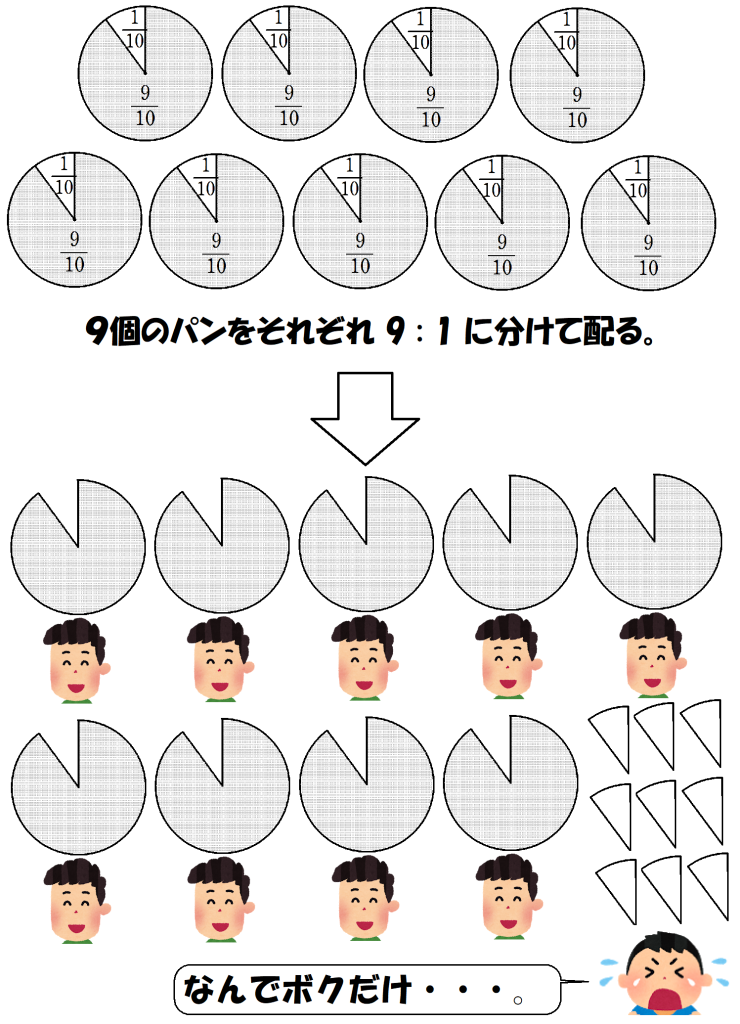
例えば、『リンド・パピルス』の問題6では、9個のパンを10人で分ける方法について解説しています。
単純に1人あたり$~\displaystyle \frac{9}{10}~$個という計算ではなく、
\frac{9}{10}=\frac{1}{2}+\frac{1}{3}+\frac{1}{15}と単位分数の和で表すことで、パンを形まで平等に分けることができました。

円周率は3.16と近似された
『リンド・パピルス』の問題50では、円形の土地の面積の求め方を解説しています。
そこでは、直径$~9~$の円の面積が$~64~$となることを、八角形への近似を使って求めていました。
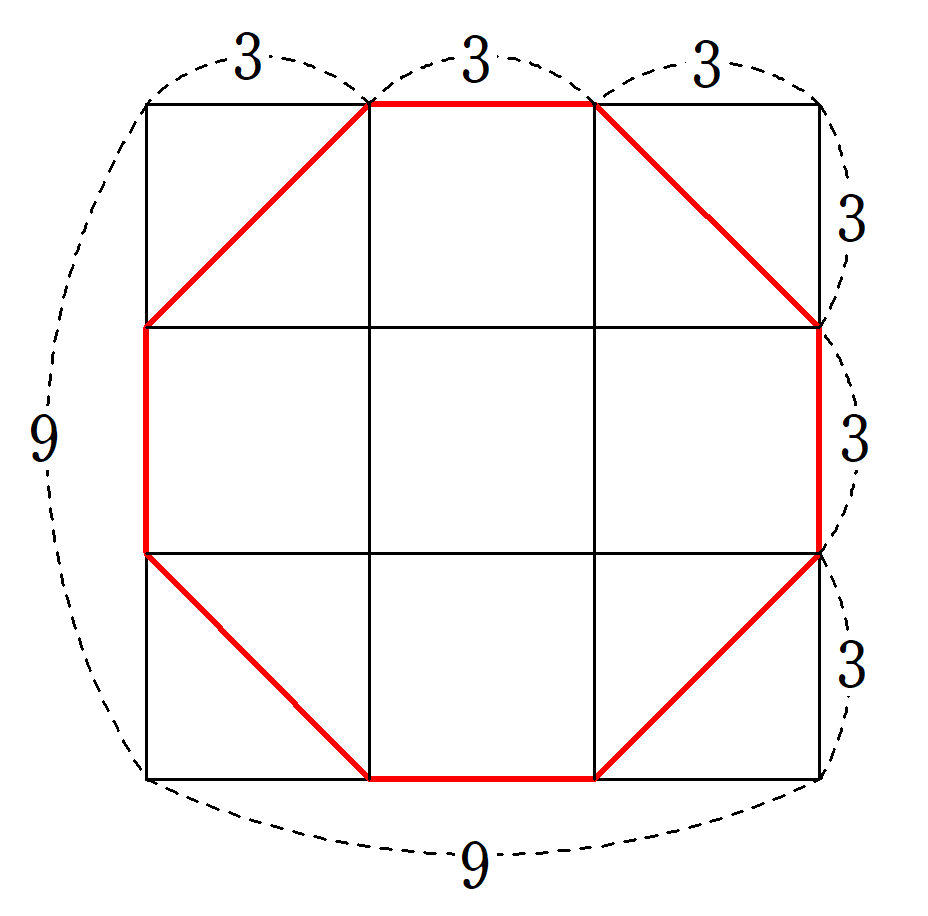
この計算結果から円周率を逆算すると$~3.16~$となり、なかなかの精度の近似であったことがわかります。

方程式は独特の方法で解いた
古代エジプトにおける方程式の問題は「アハ問題」と呼ばれ、「仮置法」という現在とは違った方法で解かれていました。
それは未知数$~x~$(アハ)に入る数を推定し、とりあえず計算をしてみた上で、元の式との比例関係を利用して解くというものです。
方程式 $~\displaystyle x+\frac{1}{4}x=15~$を解く。
$~x=4~$と仮定すると、方程式は
4+\frac{1}{4}\times 4=5 ~~~\cdots ①となるので、右辺を$~15~$にするためには、$①$の両辺を$~15 \div 5=3~$倍すればよい。
したがって、
4 \times 3 +\frac{1}{4}\times 4 \times 3=15なので、$~x=4\times 3=12~$とわかる。

まとめ・参考文献
古代エジプトの数学、とりわけ紀元前1650年の『リンド・パピルス』の内容を中心に概説してきました。
- 古代エジプトの数学は、実用性を重んじた。
- 計算をはじめ、様々な工夫を講じて問題を解き、『リンド・パピルス』という形で後世に伝わっている。
紀元前であるにも関わらず、古代エジプトが高い数学的思考力を持っていたことが全体を通してわかります。
他の四大文明の数学レベルも同等、あるいはそれ以上となっているので、年表から各記事を覗いてみてください。


紀元前1650年以降は発展しなかったのかな?



実生活に必要な数学は揃っていたため、学問としての数学はそれ以上発展しなかったんだ。
参考文献(本の紹介ページにリンクしています)
- 『カッツ 数学の歴史』,pp.4-53
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.8-20
- 『数学史 数学5000年の歩み』,pp.17-39
- 『数学の歴史物語』,pp.1-10
- 『数学の流れ30講(上)』,pp.14-24
- ピエルジョルジョ・オーディフレッディ著,河合成雄訳(2021)『幾何学の偉大なものがたり』,pp.26-38
- ポール・パーソンズ、ゲイル・ディクソン(2021)『図解教養事典 数学』,NEWTON PRESS
- 『ずかん 数字』,pp.34-50


コメント