四大文明の1つとして有名なメソポタミア文明。
メソポタミアの中にあるバビロンという都市を中心に、栄えた地域をバビロニアと言い、紀元前1750年頃には数体系が確立しました。
そのため、数学史上では「メソポタミアの数学」を「バビロニアの数学」と言い表しています。
この記事では、そのバビロニアの数学が発展していく様子を年表形式でまとめるとともに、その内容を解説。
メソポタミア文明から始まったバビロニアの数学を1つ1つ見ていきましょう。
- バビロニアの数学史の流れ
- バビロニアの数学の内容
| 時代 | B.C.4000年頃~B.C.500年頃 |
| 場所 | バビロニア(メソポタミア) |
バビロニアの数学史年表
数学史上、バビロニアとメソポタミアはほぼ同義です。
その理由は、紀元前1750年頃のハンムラビ王朝にあります。
チグリス川、ユーフラテス川の河谷地域にシュメール人が住み始める。
メソポタミア文明の始まり。「楔型文字」もこの時期にできた。
シュメール人が国家を形成。
書記たちが、土地の測量や軍備の管理のために数学を使用した。
バビロニア人がメソポタミアの主権を握る。
都市バビロンを中心とした地域「バビロニア」が広がっていった。
バビロニアのハンムラビ王朝の時代に数体系が確立。
この時代にメソポタミアの数学が出来上がり、当時の記録も残っているため、メソポタミアの数学のことをバビロニアの数学と呼ぶようになった。
様々な民族がバビロニアを侵攻した。
何度も支配者が変わり、最終的にはペルシァ人によって占領された。
完全にペルシァの支配下となり、メソポタミアの歴史が終了。
バビロニアの書記たちは、測量などの実用的な部分だけにとどまらず、趣味として数学を研究したため、古代エジプトよりも高度な内容を扱っていました。
バビロニアの数学の内容
バビロニアでは、粘土板に楔形文字を刻むことで、長期にわたって文字を保存しました。
古代エジプトのパピルスよりも丈夫であったため、たくさんの資料が現代にまで残っています。

数字は2種類のみで60進法を採用
メソポタミア文明では、紀元前4000年頃から「楔型文字」を使用しています。
古代エジプトの数字が7種類だったのに対し、楔形文字ではたったの2種類しかありません。

この2種類の数字を並べることで、$~59~$までの整数は単純に表すことができました。
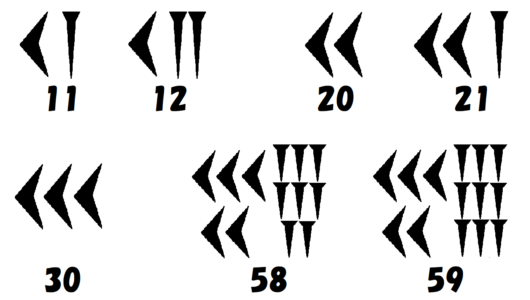
メソポタミア文明では、$~60~$進法が採用されていたため、$~60~$で位が1つ上がります。
この世界初の位取り記数法の考え方により、たった2種類の文字だけでどんなに大きな数でも表せるようになりました。
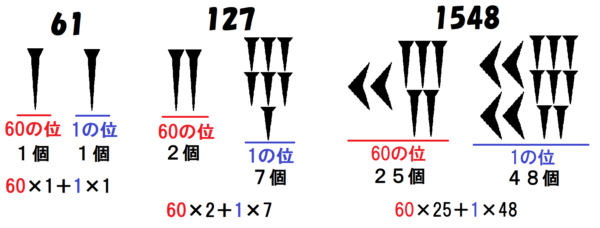
ただ、$~0~$を表す記号が無かったため、その数字が 1の位なのか 60 の位なのか、はたまた 3600の位なのかが分かりづらいという難点もありました。


小数も60進法で表した
古代エジプトが単位分数を好んだのに対し、メソポタミア文明では$~60~$進法による小数が使われました。
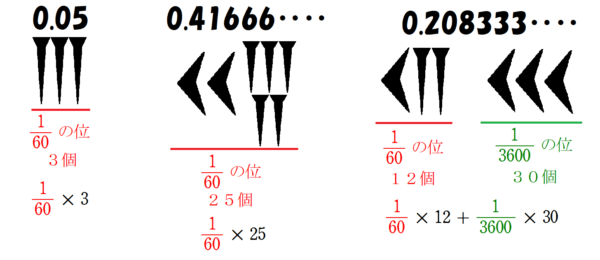
ただし、小数点や$~0~$という概念が無かったため、小数第何位かがわからないだけでなく、整数と小数の境目すらわからず、前後の文脈から数の大きさを判断するしかありませんでした。
図7のように「11」が並んでいたとしても、60の位と1の位で見るか、1の位と小数第1位で見るかは、読んだ人の勝手ということになります。
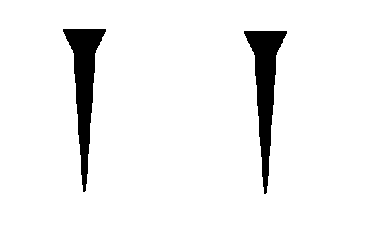

乗除は数表から探すだけ
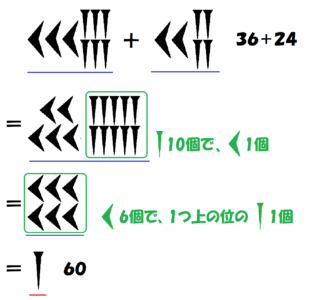
たし算・ひき算の方法は現在のやり方とほぼ変わりません。
$~10~$で繰り上がり・繰り下がりをする代わりに、$~60~$でそれを行うという違いだけです。
しかし、かけ算やわり算は数表を使って行われました。
かけ算のときに使われた積表は表9のようなもので、かけられる数に関しては40種類の数が用意されていました。
| かける数 | $1$ | $2$ | ‥‥ | $19$ |
| 積 | $2$ | $4$ | ‥‥ | $38$ |
| かける数 | $20$ | $30$ | $40$ | $50$ |
| 積 | $40$ | $1,0$※ | $1,20$ | $1,40$ |
| ※$~1,0~$は、$~60~$の位が$~1~$、$~1~$の位が$~0~$であることを表します。 | ||||
わり算のときには、積表に加えて逆数表も必要でした。
| 元の数 | $2$ | $3$ | $4$ | $5$ | $6$ |
| 逆数 | $30$ | $20$ | $15$ | $12$ | $10$ |
| 元の数 | $8$ | $9$ | $10$ | $12$ | $15$ |
| 逆数 | $7,30$ | $6,40$ | $6$ | $5$ | $4$ |
| 元の数 | $16$ | $18$ | $20$ | $24$ | $25$ |
| 逆数 | $3,45$ | $3,20$ | $3$ | $2,30$ | $2,24$ |
| 元の数 | $27$ | $30$ | $32$ | $36$ | $40$ |
| 逆数 | $2,13,20$ | $2$ | $1,52,30$ | $1,40$ | $1,30$ |
| 元の数 | $45$ | $48$ | $50$ | $54$ | $1$ |
| 逆数 | $1,20$ | $1,15$ | $1,12$ | $1,6,40$ | $1$ |
| 元の数 | $1,4$ | $1,12$ | $1,15$ | $1,20$ | $1,21$ |
| 逆数 | $56,15$ | $50$ | $48$ | $45$ | $44,26,40$ |
逆数表でかけ算に直し、その後積表を使って計算をするという流れでわり算をしていました。
逆数表は小数点のない数字の羅列だったため、当時のバビロニア人は位取りによる計算ミスが多かったことも粘土板からわかっています。

「仮置法」で連立方程式を解いた
未知数が$~x~$のみの一次方程式については、現在と同様、移項などの等式変形を使って解いていたと思われ、バビロニア人にとっては解けて当たり前の問題となっていました。
粘土板に詳しく解説されていたのは、$~x~$と$~y~$の連立方程式の解き方についてです。
連立方程式
\begin{cases}
&\displaystyle \frac{2}{3}x-\frac{1}{2}y=500~~~\cdots ① \\
&x+y=1800~~~\cdots ②
\end{cases}について、
$②$より、$~x=900~,~y=900~$と仮定する。
$①$の左辺に代入すると、
\frac{2}{3}\cdot 900-\frac{1}{2}\cdot 900=150で、$①$の右辺との差は$~350~$である。
ここで、$~x~$を$~1~$増やし、$~y~$を$~1~$減らすことを考えると、
\frac{2}{3}\cdot 1+\frac{1}{2}\cdot 1=\frac{7}{6}なので、$~350~$の差を縮めるためには
350 \div \frac{7}{6}=300より、$~x~$を$~300~$増やし、$~y~$を$~300~$減らせばよい。
したがって、
\begin{cases}&x=900+300=1200 \\&y=900-300=600\end{cases}と求まる。
このように、古代エジプトの仮置法のような方法で、連立方程式を華麗に解くことができました。

二次方程式は3つのパターンに分類
当時は$~0~$や負の数が無かったため、二次方程式は以下の3つのパターンに分けられました。
\begin{cases}
(1)~&x^2-px-q=0 \\
(2)~&x^2+px-q=0 ~~~~~~~(p,q~は正の定数) \\
(3)~&x^2-px+q=0
\end{cases}$(1)$のパターンであれば、以下のような式変形によって、解を導いています。
- $~p~$の半分をとり、$~\displaystyle \frac{p}{2}~$
- $~\displaystyle \frac{p}{2}~$に$~\displaystyle \frac{p}{2}~$をかけて、$~\displaystyle \frac{p^2}{4}~$
- これに$~q~$をたすと、$~\displaystyle \frac{p^2}{4}+q~$
- これは、$~\displaystyle \sqrt{\frac{p^2}{4}+q}~$の平方
- ここで、$~\displaystyle \frac{p}{2}~$を$~\displaystyle \sqrt{\frac{p^2}{4}+q}~$をにたして、$~\displaystyle \sqrt{\frac{p^2}{4}+q}+\frac{p}{2}$
最後に出てくる式を見ると、二次方程式の解の公式と同じ形をしていることがわかります。
ただし、負の解が出ないように$~\sqrt{}~$の符号は$~\pm~$ではなく、$~+~$限定です。

ピタゴラス数の研究が細かい
バビロニアでは、ピタゴラス数について研究されました。
そのことが、紀元前1800年頃に書かれたと推定される粘土板プリンプトン322からわかります。

(出典:photo author unknown, Public domain, via Wikimedia Commons)
プリンプトン322は、$~a^2+b^2=c^2~$を満たす数の組$~(a,b,c)~$の値の数表となっています。
長さが$~c~$と$~a~$の辺のなす角を$~\theta~$とすると、プリンプトン322の数表は$~\theta~$の値が等差数列的に減少していることが窺えます。
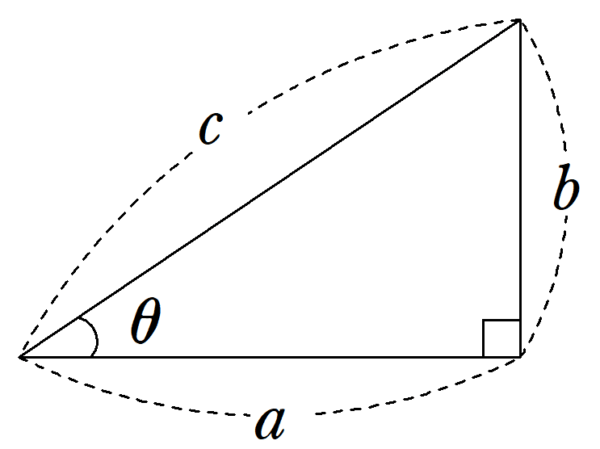
このことから、バビロニア人は単にピタゴラス数の研究をしていただけでなく、三平方の定理を意識していたことがわかります。
ピタゴラス(Pythagoras, B.C.569頃-B.C.500頃)が生まれる1000年以上前から、定理自体は知られていた証拠と言えるでしょう。

相加相乗平均を使って√ の近似値を求めた
三平方の定理や二次方程式で避けられないのが、平方根。
粘土板YBC7289では、$~30\sqrt{2}~$の値を見ることができます。

(出典:Bill Casselman, CC BY-SA 3.0, via Wikimedia Commons)
実際、$~\sqrt{2}~$の近似値は以下のように求めました。
$~\sqrt{2}~$の近似値として、$~a_1=1.5~$を見積もる。
$~\displaystyle \frac{2}{a_1}=\frac{2}{1.5}=\frac{4}{3}~$を考えると、
\frac{2}{a_1} < \sqrt{2} < a_1 となる。
次に、$~a_2~$を下のように定義する。
a_2=\frac{1}{2}\left(a_1+\frac{2}{a_1} \right)=\frac{1}{2}\left( \frac{3}{2}+\frac{4}{3} \right)=\frac{17}{12}この$~a_2=\displaystyle \frac{17}{12} \fallingdotseq 1.416 \cdots~$は、$~a_1~$より小さく、$~\sqrt{2}~$以上になるため、$~a_1~$よりも$~\sqrt{2}~$を高い精度で近似している。
これを、
\begin{align*}a_3&=\frac{1}{2}\left(a_2+\frac{2}{a_2} \right) \\
\\
a_4&=\frac{1}{2}\left(a_3+\frac{2}{a_3} \right) \\
\end{align*}と続けていくことにより、$~\sqrt{2}~$をより高い精度で近似することができる。
この方法で、
\sqrt{2}=1.41421296\cdotsという値を導きました。
まとめ
メソポタミア文明の数学、すなわちバビロニアの数学について概説してきました。
- 研究好きな書記たちが、数学を実用的な範囲外まで発展させた。
- 60進法でありながら、数表を使って多様な計算を行っていた。
- 二次方程式や三平方の定理といった高度な内容まで扱っていた。
いろいろな種類の数表を武器に、バビロニア人は実生活の範囲を超えて数学を発展させました。
バビロニアの書記たちは、それ以後の数学に、抽象的な考え方をする学問という性質を持たせたと言えるでしょう。


解の公式ってこんな昔からあったんだ~。



負の数がないから、場合分けをしているところがすごいよね。


コメント